题目内容
10.已知a、b均为有理数,且关于x的方程为$\frac{ax+ab}{96}$=$\frac{x-|b|}{12}$+1.(1)当a=4,b=-$\frac{1}{2}$时,求x的值;
(2)若关于x的方程有无数个解.
①求a、b的值;
②设线段AB=a,CD=b,线段CD在直线AB上(A在B的左侧,C在D的左侧),且M、N分别是线段AC、BD的中点,若BC=4,求MN的值.
分析 (1)把a=4,b=-$\frac{1}{2}$代入得到关于x的方程,解方程即可求得x;
(2)①由$\frac{ax+ab}{96}$=$\frac{x-|b|}{12}$+1可得(a-8)x=-8|b|-ab+96,根据关于x的方程有无数个解,可得a-8=0,-8|b|-ab+96=0,解方程即可求解;
②分三种情况:点C、D都在点A的左侧,点C在点A的左侧且点D在点A的右侧时,线段CD在线段AB上时;点C在点B的左侧,点D在点B的右侧时;点C、D都在点B的右侧时;进行讨论可求MN的值.
解答 解:(1)当a=4,b=-$\frac{1}{2}$时,方程变为$\frac{4x-2}{96}$=$\frac{x-\frac{1}{2}}{12}$+1,
化简,得$\frac{2x-1}{48}$=$\frac{2x-1}{24}$+1,
去分母,得2x-1=4x-2+48,
-2x=47,
x=-$\frac{47}{2}$;
(2)①去分母,得ax+ab=8x-8|b|+96,
(a-8)x=-8|b|-ab+96,
∵关于x的方程有无数个解,
∴a-8=0,-8|b|-ab+96=0,
解得a=8,
则-8|b|-8b+96=0,
当b≥0时,得-16b+96=0,
解得b=6,
当b<0时,得8b-8b+96=0,无解.
综上可知,a=8,b=6.
②依题意有AB=8,CD=6,
当点C、D都在点A的左侧,点C在点A的左侧且点D在点A的右侧时,线段CD在线段AB上时,这三种情况均有BC>CD,不合题意;
当点C在点B的左侧,点D在点B的右侧时,如图所示: ,
,
有BC<CD,符合题意;
∵BC=4,CD=6,
∴BD=2,
∵N是线段BD的中点,
∴BN=1,
∴CN=CB+BN=4+1=5,
∵AB=8,
∴CM=$\frac{1}{2}$AC=2,
∴MN=CM+CN=2+5=7;
当点C、D都在点B的右侧时,符合题意,如图所示: ;
;
则AC=AB+BC=8+4=12,BD=BC+CD=4+6=10,
∵M、N分别是线段AC、BD的中点,
∴CM=$\frac{1}{2}$AC=6,BN=$\frac{1}{2}$BD=5,
∴MN=CM+BN-BC=6+5-4=7.
综上所述,MN的值为7.
点评 此题考查了两点间的距离,一元一次方程的解,在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.

 名校课堂系列答案
名校课堂系列答案(1)试用含有x的代数式表示售价c;
(2)若小华的妈妈想买8千克这种货物,那么她需要付多少钱?
| 销售量x(千克) | 销售价c(元) |
| 1 | 2+0.1 |
| 2 | 4+0.2 |
| 3 | 6+0.3 |
| 4 | 8+0.4 |
| … | … |
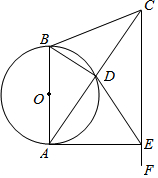 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,AE恰为⊙O的切线.(1)试说明:△CBA∽△CDE;
(2)若AB=3,BD=2,求AE的长.
①两点确定一条直线;
②一条直线有且只有一条垂线;
③不相等的两个角一定不是对顶角;
④若|a|=-a,则a<0;
⑤若a,b互为相反数,则a,b的商必定等于-1.
其中正确的是①③.(请填序号)
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
| A. | 0.58×105 | B. | 12.3×107 | C. | 12×103 | D. | 8.0×108 |

 如图,∠AOC=∠BOD,∠AOD=120°,∠BOC=70°,求∠AOB的度数.
如图,∠AOC=∠BOD,∠AOD=120°,∠BOC=70°,求∠AOB的度数. 如图,测量小玻璃管口径的量具ABC,AB的长为30cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是20cm.
如图,测量小玻璃管口径的量具ABC,AB的长为30cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是20cm.