题目内容
6.若△ABC的面积36,AB=5,BC=6,AC=7,求内切圆的半径.分析 如图,⊙O为△ABC的内切圆,连结OA、OB、OC、OD,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,设⊙O的半径为r,根据切线的性质得OD=OE=OF=r,然后根据三角形面积公式,利用S△AOC+S△AOB+S△BOC=S△ABC,可得$\frac{1}{2}$•r•7+$\frac{1}{2}$•r•5+$\frac{1}{2}$•r•6=36,再解关于r的方程即可.
解答 解: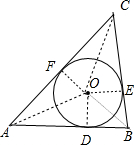 如图,⊙O为△ABC的内切圆,连结OA、OB、OC、OD,
如图,⊙O为△ABC的内切圆,连结OA、OB、OC、OD,
作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,设⊙O的半径为r,则OD=OE=OF=r,
∵S△AOC+S△AOB+S△BOC=S△ABC,
∴$\frac{1}{2}$•r•7+$\frac{1}{2}$•r•5+$\frac{1}{2}$•r•6=36,
∴r=4,
即△ABC内切圆的半径为4.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
15.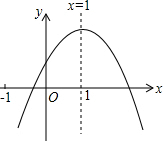 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①abc>0;②a-b+c<0;③当x<0时,y<0;④9a2+3b+c<0;⑤2a-b-1<0.
其中错误的结论的个数有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a-b+c<0;③当x<0时,y<0;④9a2+3b+c<0;⑤2a-b-1<0.
其中错误的结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知两圆的圆心距为5,两圆的半径分别是方程x2-6x+5=0的两根,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
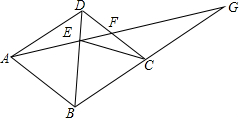 已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.
已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.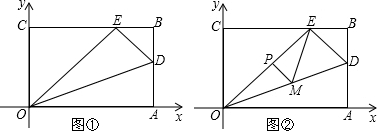
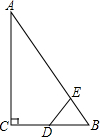 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).