题目内容
16.在△ABC中,∠ACB=90°,AC=BC.(1)如图1,当点P是线段上异于A、B的任一点,求证:AP2+BP2=2PC2;
(提示:可将三角形BPC绕点C顺时针方向旋转90°,得到三角形ADC,连接PD…)
(2)如图2,当P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.
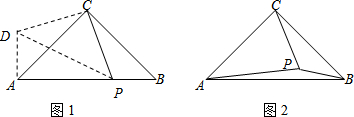
分析 (1)将三角形BPC绕点C顺时针方向旋转90°,得到三角形ADC,连接PD,得出AD=PB,CD=CP,∠DAC=∠CBP,∠DCA=∠BCP,得出△DAP和△CDP是直角三角形,利用勾股定理得出答案即可;
(2)根据旋转的性质得到CP=CD=2,∠DCP=90°,DB=PA=3,则△CPD为等腰直角三角形,利用等腰直角三角形的性质得PD=$\sqrt{2}$PC=2$\sqrt{2}$,∠CPD=45°,在△PDB中,PB=1,PD=$\sqrt{2}$,DB=3,易得PB2+PD2=BD2,根据勾股定理的逆定理得到△PBD为直角三角形,即可得到∠BPC的度数
解答 (1)证明:将三角形BPC绕点C顺时针方向旋转90°,得到△ADC,
因此AD=PB,CD=CP,∠DAC=∠CBP,∠DCA=∠BCP,
∵∠ACB=90°,
∴∠DCP=90°,∠DAP=90°,
∴△DAP和△CDP是直角三角形,
∴AP2+AD2=PD2;CP2+CD2=PD2;
∴AP2+BP2=2PC2;
(2)解:如图,
把△ACP绕点C逆时针旋转90°得到△BCD,连接DP,
∵△ACP绕点C逆时针旋转90°得到△BCD,
∴CP=CD=2,∠DCP=90°,DB=PA=3,
∴△CPD为等腰直角三角形,
∴PD=$\sqrt{2}$PC=2$\sqrt{2}$,∠CPD=45°,
在△PDB中,PB=1,PD=2$\sqrt{2}$,DB=3,
而12+(2$\sqrt{2}$)2=32,
∴PB2+PD2=BD2,
∴△PBD为直角三角形,
∴∠DPB=90°,
∴∠BPC=45°+90°=135°.
点评 本题考查了旋转的性质:旋转前后两个图形全等,即对应角相等,对应线段相等;也考查了等腰直角三角形的性质以及勾股定理以及逆定理的运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,∠ABC为直角,BC长为3,AB长为4,AF长为12,正方形的面积为169,求三角形AFC的面积.
如图,∠ABC为直角,BC长为3,AB长为4,AF长为12,正方形的面积为169,求三角形AFC的面积.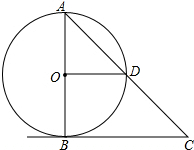 如图,AB是⊙O的直径,BC是切线,BC=2OB,AC与⊙O相交于点D,求证:OD⊥AB.
如图,AB是⊙O的直径,BC是切线,BC=2OB,AC与⊙O相交于点D,求证:OD⊥AB.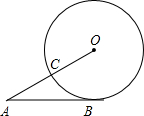 已知:如图,AB切⊙O于点B,OA交⊙O于点C,∠A=30°,AC=4,求⊙O的半径r及AB的长.
已知:如图,AB切⊙O于点B,OA交⊙O于点C,∠A=30°,AC=4,求⊙O的半径r及AB的长. 如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为S1、S2、S3.若S1+S3=10,则S2的值为4.
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ、△DKM、△CNH的面积依次为S1、S2、S3.若S1+S3=10,则S2的值为4. 如图,点E是正方形ABCD对角线BD上一个动点,以CE为腰作等腰直角三角形ECF,使∠ECF=90°,点E在BD上移动时(与B,D都不重合),判断△DEF的形状?为什么?
如图,点E是正方形ABCD对角线BD上一个动点,以CE为腰作等腰直角三角形ECF,使∠ECF=90°,点E在BD上移动时(与B,D都不重合),判断△DEF的形状?为什么? 如图,直线1经过矩形ABCD的对称中心O,分别过点A和点C作直线1的垂线,垂足分别为E和F.求证:OE=OF.
如图,直线1经过矩形ABCD的对称中心O,分别过点A和点C作直线1的垂线,垂足分别为E和F.求证:OE=OF.