题目内容
1.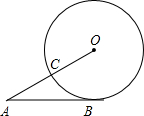 已知:如图,AB切⊙O于点B,OA交⊙O于点C,∠A=30°,AC=4,求⊙O的半径r及AB的长.
已知:如图,AB切⊙O于点B,OA交⊙O于点C,∠A=30°,AC=4,求⊙O的半径r及AB的长.
分析 连结OB,如图,根据切线的性质得∠ABO=90°,在Rt△AOB中利用含30°的直角三角形三边的关系得到r=$\frac{1}{2}$(r+4),解得r=4,则AB=$\sqrt{3}$OB=4$\sqrt{3}$.
解答 解:连结OB,如图,
∵AB切⊙O于点B,
∴OB⊥AB,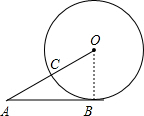
∴∠ABO=90°,
在Rt△AOB中,∵∠A=30°,
∴OB=$\frac{1}{2}$OA,即r=$\frac{1}{2}$(r+4),
∴r=4,
∴AB=$\sqrt{3}$OB=4$\sqrt{3}$.
答:⊙O的半径r和AB的长分别为4、4$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列方程中,是一元二次方程的个数有( )
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.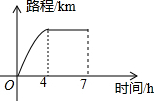 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )| A. | 前4h中汽车的速度越来越快 | B. | 4h后汽车静止不动 | ||
| C. | 4h后汽车以相同的速度行驶 | D. | 前4h汽车以相同速度行驶 |
 如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )
如图,是由几个相同的小正方体组成的几何体,则它的左视图是( )



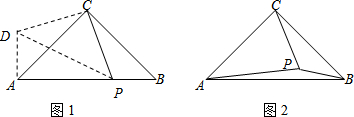
 如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF.
如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF.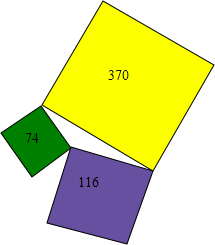 如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?
如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少? 如图,已知△ABC中,△ABC的平分线AD与BC边相交于点D,过点D分别作AB、AC的平行线交AC、AB于E、F.联结EF与CB的延长线相交于点G.
如图,已知△ABC中,△ABC的平分线AD与BC边相交于点D,过点D分别作AB、AC的平行线交AC、AB于E、F.联结EF与CB的延长线相交于点G.