题目内容
4.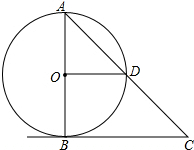 如图,AB是⊙O的直径,BC是切线,BC=2OB,AC与⊙O相交于点D,求证:OD⊥AB.
如图,AB是⊙O的直径,BC是切线,BC=2OB,AC与⊙O相交于点D,求证:OD⊥AB.
分析 根据切线的性质得∠ABC=90°,由于BC=2OB,则可判断△ABC为等腰直角三角形,所以∠A=45°,于是得到∠ODA=∠A=45°,则∠AOD=90°,然后根据垂直的定义即可得到OD⊥AB.
解答 证明:∵BC是切线,
∴AB⊥BC,
∴∠ABC=90°,
∵BC=2OB,
∴CB=AB,
∴△ABC为等腰直角三角形,
∴∠A=45°,
∵OA=OD,
∴∠ODA=∠A=45°,
∴∠AOD=90°,
∴OD⊥AB.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.将面积为a2的正方形边长增加2,则正方形的面积增加了( )
| A. | 4 | B. | 2a+4 | C. | 4a+4 | D. | 4a |
12.下列方程中,是一元二次方程的个数有( )
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
(1)$\sqrt{3}$x2+2x+1=0
(2)$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0
(3)x2-2x+1=0
(4)(a-1)x2+bx+c=0
(5)x2+x=4-x2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.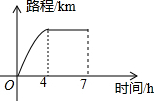 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
 一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )
一辆汽车行驶的路程与行驶时间的关系如图所示,下列说法正确的是( )| A. | 前4h中汽车的速度越来越快 | B. | 4h后汽车静止不动 | ||
| C. | 4h后汽车以相同的速度行驶 | D. | 前4h汽车以相同速度行驶 |
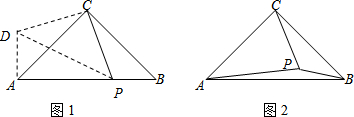
 如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF.
如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF. 如图,点B是由点A作轴对称变换得到的,请画出对称轴.
如图,点B是由点A作轴对称变换得到的,请画出对称轴.