题目内容
5. 如图,点E是正方形ABCD对角线BD上一个动点,以CE为腰作等腰直角三角形ECF,使∠ECF=90°,点E在BD上移动时(与B,D都不重合),判断△DEF的形状?为什么?
如图,点E是正方形ABCD对角线BD上一个动点,以CE为腰作等腰直角三角形ECF,使∠ECF=90°,点E在BD上移动时(与B,D都不重合),判断△DEF的形状?为什么?
分析 由正方形的性质可知:∠DBC=∠BDC=45°,然后证明△BEC≌△DFC,从而得到∠EBC=∠FDC=45°,从而可求得∠BDF=90°.
解答 解:∵四边形ABCD是正方形,
∴∠DBC=∠BDC=45°.
∵∠BCE+∠ECD=90°,∠ECD+∠DCF=90°,
∴∠ECB=∠FCD.
在△BEC和△DFC中,$\left\{\begin{array}{l}{CB=DC}\\{∠ECB=∠DCF}\\{CE=CF}\end{array}\right.$,
∴△BEC≌△DFC.
∴∠EBC=∠FDC=45°.
∴∠BDF=90°.
∴△DEF是直角三角形.
点评 本题主要考查的是正方形的性质、全等三角形的性质和判断,证得△BEC≌△DFC是解题的关键.

练习册系列答案
相关题目
20.如果x是有理数,那么( )
| A. | 1-x的值一定比1小 | B. | 1-x2的值一定比1小 | ||
| C. | 1-x的值一定不大于1 | D. | 1-x2的值不大于1 |
根据国家发改委实施“阶梯电价”的有关文件要求,某市决定从2013年4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
不超过180千瓦时的部分 | a |
超过180千瓦时的部分 | b |
2013年5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费121元.
(1)上表中,a= ;b= ;(2)随着夏天的到来,用电量将增加.为了节省开支,该市居民小王计划把今年6月份的电费控制在不超过家庭月收入的2%.若小王家庭月收入为9300元,则小王家今年6月份最多能用电多少千瓦时?
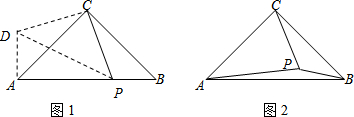
 如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF.
如图,DE∥AB,DF∥AE,求证:CE•BE=CB•EF.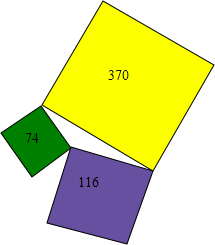 如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?
如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少? 如图,点B是由点A作轴对称变换得到的,请画出对称轴.
如图,点B是由点A作轴对称变换得到的,请画出对称轴.