题目内容
19.已知$x=2-\sqrt{3}$,求$\frac{{1-2x+{x^2}}}{x-1}-\frac{{\sqrt{{x^2}-2x+1}}}{{{x^2}-x}}$.分析 首先化简所求二次根式,然后代入即可.
解答 解:$\frac{1-2x{+x}^{2}}{x-1}-\frac{\sqrt{{x}^{2}-2x+1}}{{x}^{2}-x}$
=$\frac{{(1-x)}^{2}}{x-1}$-$\frac{\sqrt{(x-1)^{2}}}{x(x-1)}$
=x-1-$\frac{1-x}{x(x-1)}$
=x-1$+\frac{1}{x}$,
将$x=2-\sqrt{3}$,代入得:x-1$+\frac{1}{x}$=2-$\sqrt{3}$-1$+\frac{1}{2-\sqrt{3}}$=1-$\sqrt{3}$$+2+\sqrt{3}$=3,
∴原式的值为3.
点评 此题主要考查了二次根式的化简,先化简再代入,注意因式分解和绝对值的化简是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
现要配制这种营养食品20千克,要求每千克至少含有9600单位的维生素C.设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
| 原料 维生素C及价格 | 甲种原料 | 乙种原料 |
| 维生素C(单位/千克) | 600 | 400 |
| 原料价格(元/千克) | 9 | 5 |
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?
11.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y+2=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=1}\\{xy=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=x}\\{x-2y=1}\end{array}\right.$ |
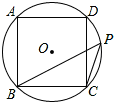 如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.
如图,正方形ABCD的四个顶点分别在⊙O上,点P在$\widehat{CD}$上不同于点C的任意一点,则∠BPC的度数是45°.