题目内容
16.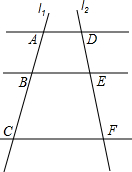 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,$\frac{DE}{EF}=\frac{2}{5}$,AC=14;
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,$\frac{DE}{EF}=\frac{2}{5}$,AC=14;(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
分析 (1)由平行线分线段成比例定理和比例的性质得出$\frac{AB}{AC}=\frac{2}{7}$,即可求出AB的长,得出BC的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,得出AD=HE=GF=7,由平行线分线段成比例定理得出比例式求出BH,即可得出结果.
解答 解:(1)∵AD∥BE∥CF,
∴$\frac{AB}{BC}=\frac{DE}{EF}=\frac{2}{5}$,
∴$\frac{AB}{AC}=\frac{2}{7}$,
∵AC=14,∴AB=4,
∴BC=14-4=10;
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示: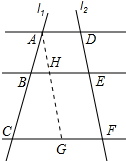
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14-7=7,
∵BE∥CF,
∴$\frac{BH}{CG}=\frac{AB}{AC}=\frac{2}{7}$,
∴BH=2,
∴BE=2+7=9.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
| A. | $sinA=\frac{{\sqrt{3}}}{2}$ | B. | $cosA=\frac{{\sqrt{3}}}{2}$ | C. | $tanA=\frac{1}{2}$ | D. | $cotA=\frac{{\sqrt{3}}}{3}$ |
5.下列语句正确的是( )
| A. | -b2的系数是1,次数是2 | B. | 3a+2b的项数是2,次数是2 | ||
| C. | 4a2+b2+1的项数是2,次数是2 | D. | $\frac{1}{{x}^{2}}$不是单项式 |
 如图,直线AD∥BE∥CF,$BC=\frac{2}{3}AB$,DE=6,那么EF的值是4.
如图,直线AD∥BE∥CF,$BC=\frac{2}{3}AB$,DE=6,那么EF的值是4.