题目内容
11.抛物线y=(a+2)x2+3x-a的开口向下,那么a的取值范围是a<-2.分析 根据抛物线y=(a+2)x2+3x-a的开口向下,可得a+2<0,从而可以得到a的取值范围.
解答 解:∵抛物线y=(a+2)x2+3x-a的开口向下,
∴a+2<0,
得a<-2,
故答案为:a<-2.
点评 本题考查二次函数的性质和定义,解题的关键是明确二次函数的开口向下,则二次项系数就小于0.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.已知$\frac{a}{b}$=$\frac{2}{3}$,那么$\frac{a}{a+b}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
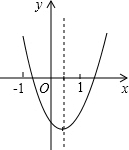 二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,这五个代数式中,其值一定是正数的有( )
二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,这五个代数式中,其值一定是正数的有( )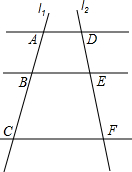 如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,$\frac{DE}{EF}=\frac{2}{5}$,AC=14;
如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,$\frac{DE}{EF}=\frac{2}{5}$,AC=14;