题目内容
15．计算：$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+2}…+\frac{1}{\sqrt{n}+\sqrt{n+1}}$．分析 首先找出二次根式的有理化因式，进而将各二次根式化简求出即可．
解答 解：$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+2}…+\frac{1}{\sqrt{n}+\sqrt{n+1}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{3}$-2+…+$\sqrt{n+1}$-$\sqrt{n}$
=$\sqrt{n+1}$-1．
点评 此题主要考查了分母有理化，正确化简二次根式是解题关键．
练习册系列答案
相关题目
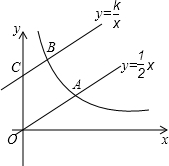如图，直线$y=\frac{1}{2}x$与双曲线$y=\frac{k}{x}$（k＞0，x＞0）交于点A，将直线$y=\frac{1}{2}x$向上平移4个单位长度后，与y轴交于点C，与双曲线$y=\frac{k}{x}$（k＞0，x＞0）交于点B．
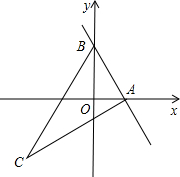已知：如图，直线y=kx+2与x轴正半轴相交于A（t，0），与y轴相交于点B，抛物线y=-x2+bx+c经过点A和点B，点C在第三象象限内，且AC⊥AB，tan∠ACB=$\frac{1}{2}$．
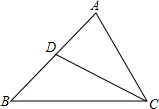如图，在△ABC中，CD是AB边上的中线，已知∠B=45°，tan∠ACB=3，AC=$\sqrt{10}$，求tan∠DCB的值．
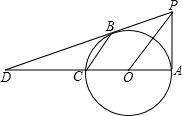以AC=6为直径画一个圆，过点A作AP⊥AC，过点C作CB∥OP，直线PB与直线AC相交于点D．