Question

14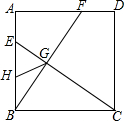．如图，在正方形ABCD中，点E、F分别在AB、AD边上，且BE=AF，连接CE、BF，它们相交于点G，点H为线段BE的中点，连接GH．若∠EHG=$\frac{4}{3}$∠DCE，则∠ABF是36度．

Answer 1

分析 先证明△ABF≌△BCE，得出∠ABF=∠BCE，再由∠ABF+∠CBG=90°，证出∠BGC=90°，得出∠BGE=90°，由点H为线段BE的中点，得出∠GEH=∠HGE，∠HBG=∠HGB，设∠DCE=3x，则∠EHG=4x，得出∠ABF=2x，根据三角形内角和定理得方程：3x+4x+3x=180°，解方程即可得出结果．

解答 解：∵四边形ABCD是正方形，
∴∠A=∠ABC=90°，AB=BC，
在△ABF和△BCE中，
$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠A=∠ABC}&{\;}\\{AF=BE}&{\;}\end{array}\right.$，
∴△ABF≌△BCE（SAS），
∴∠ABF=∠BCE，
∵∠ABF+∠CBG=90°，
∴∠CBG+∠BCE=90°，
∴∠BGC=90°，
∴∠BGE=90°，
∵点H为线段BE的中点，
∴GH=$\frac{1}{2}$BE=EH=BH，
∴∠GEH=∠HGE，∠HBG=∠HGB，
∵∠EHG=$\frac{4}{3}$∠DCE，
设∠DCE=3x，则∠EHG=4x，
∵AB∥CD，
∴∠HEG=∠DCE=3x，
∴∠HGE=3x，∠ABF=2x，
∵在△HGE中，3x+4x+3x=180°，
解得：x=18°，
∴∠ABF=36°．

点评 本题考查了正方形的性质、全等三角形的判定与性质以及直角三角形斜边上的中线性质；通过证明三角形全等证出CE⊥BF是解决问题的关键．