题目内容
4.化简求值$\frac{a-b}{{{a^2}+ab}}÷\frac{{ab-{a^2}}}{{{a^2}{b^2}-{a^4}}}$,其中a=3,b=-1.分析 先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可.
解答 解:原式=$\frac{a-b}{a(a+b)}$•$\frac{-{a}^{2}(a+b)(a-b)}{-a(a-b)}$
=$\frac{a-b}{a(a+b)}$•a(a+b)
=a-b,
当a=3,b=-1时,原式=3+1=4.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
14.在一次九年级学生视力检查中.随机检查了8个人的右眼视力,结果如下:4.0,4.2,4.5,4.0,4.4,4.5,4.0,4.8.则下列说法中正确的是( )
| A. | 这组数据的中位数是4.4 | B. | 这组数据的众数是4.5 | ||
| C. | 这组数据的平均数是4.3 | D. | 视力为4.0的频率为0.3 |
9.化简:(-m)12÷(-m)3等于( )
| A. | m4 | B. | -m4 | C. | m9 | D. | -m9 |
 如图,已知∠1=63°,∠A=117°,问:直线AB与CD平行吗?为什么?
如图,已知∠1=63°,∠A=117°,问:直线AB与CD平行吗?为什么?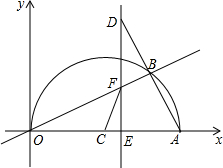 平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.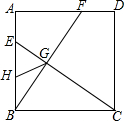 如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.
如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.