题目内容
9.函数y=$\frac{2}{x}$与y=x-3的图象有一个交点的坐标为(a,b),求$\frac{2a+3ab-2b}{b-2ab-a}$的值.分析 由y=$\frac{2}{x}$与y=x-3函数交点坐标为(a,b),将x=a,y=b代入反比例与一次函数解析式,得到ab及a-b的值,将所求式子变形后,把ab及a-b的值代入即可求出值.
解答 解:∵y=$\frac{2}{x}$与y=x-3函数交点坐标为(a,b),
∴将x=a,y=b代入y=$\frac{2}{x}$得:b=$\frac{2}{a}$,即ab=2,
代入y=x-3得:b=a-3,即a-b=3,
则$\frac{2a+3ab-2b}{b-2ab-a}$=$\frac{2(a-b)+3ab}{-(a-b)-2ab}$=$\frac{2×3+3×2}{-3-2×2}$=-$\frac{12}{7}$.
点评 此题考查了反比例函数与一次函数的交点问题,利用了整体代入的思想,根据题意得出ab与a-b的值是解本题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.顺次连接对角线相等的四边形的各边中点,所得图形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
18.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的面积之和是78cm2,那么较大的多边形的面积是( )
| A. | 44.8 | B. | 42 | C. | 52 | D. | 54 |
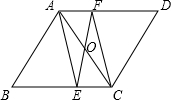 在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.
在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.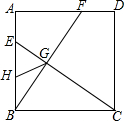 如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.
如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.