题目内容
5. 小麦与小辉在玩游戏,她们定义了一种新的规则,用象棋的“相”、“仕”、“帅”、“兵”来比较大小.共有10个棋子:2个“相”,2个“仕”,1个“帅”,5个“兵”.游戏规则如下:
小麦与小辉在玩游戏,她们定义了一种新的规则,用象棋的“相”、“仕”、“帅”、“兵”来比较大小.共有10个棋子:2个“相”,2个“仕”,1个“帅”,5个“兵”.游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一只棋进行比赛称一轮比赛,先摸者摸出的棋不放回;
②“相”胜“兵”;“仕”胜“相”、“兵”;“帅”胜“相”、“仕”;“兵”胜“帅”;
③相同棋子不分胜负.
(1)若小麦先摸,问小麦摸到“仕”的概率是多少?
(2)小麦先摸到了“仕”,小辉在剩余的9只棋中随机摸一只,问这一轮中小麦胜小辉的概率是多少?
(3)小麦先摸一只棋,小辉在剩余的9只棋中随机摸一只,问这一轮中小麦希望摸到哪种棋胜的概率最大?
分析 (1)由共有10个棋子:2个“相”,2个“仕”,1个“帅”,5个“兵”,直接利用概率公式求解即可求得答案;
(2)由小麦先摸到了“仕”,“仕”胜“相”、“兵”;可得这一轮中小麦胜小辉的有7种情况,然后利用概率公式求解即可求得答案;
(3)首先分别求得摸到“相”、“仕”;“兵”“帅”胜的概率,比较即可求得答案.
解答 解:(1)小麦摸到“仕”的概率为:$\frac{2}{10}$=$\frac{1}{5}$;
(2)∵小麦先摸到了“仕”,“仕”胜“相”、“兵”;
∴这一轮中小麦胜小辉的有7种情况,
∴这一轮中小麦胜小辉的概率为:$\frac{7}{9}$;
(3)①摸到“相”胜的概率为:$\frac{5}{9}$;
②摸到“仕”胜的概率为:$\frac{7}{9}$,
③摸到“帅”胜的概率为:$\frac{4}{9}$,
④摸到“兵”胜的概率为:$\frac{1}{9}$;
∴摸到“仕”胜的概率最高.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在Rt△ABC中,∠C=90°,若斜边上的高为h,sinA=$\frac{3}{5}$,则AB的长等于( )
| A. | $\frac{5}{4}$h | B. | $\frac{5}{3}$h | C. | $\frac{25}{12}$h | D. | $\frac{12}{25}$h |
 如图,已知∠1=63°,∠A=117°,问:直线AB与CD平行吗?为什么?
如图,已知∠1=63°,∠A=117°,问:直线AB与CD平行吗?为什么?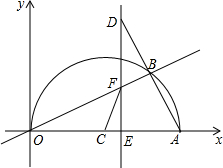 平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
平面直角坐标系中,已知点A的坐标为(10,0),已知点C为中点,以c为圆心作圆,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.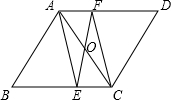 在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.
在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.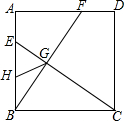 如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.
如图,在正方形ABCD中,点E、F分别在AB、AD边上,且BE=AF,连接CE、BF,它们相交于点G,点H为线段BE的中点,连接GH.若∠EHG=$\frac{4}{3}$∠DCE,则∠ABF是36度.