题目内容
17．计算：（$\sqrt{2}$）2=2，$\sqrt{（\frac{2}{3}）^{2}}$=$\frac{2}{3}$，$\sqrt{（-2）^{2}}$=2．分析 根据二次根式的性质，即可解答．
解答 解：$（\sqrt{2}）^{2}$=2，$\sqrt{（\frac{2}{3}}）^{2}=\frac{2}{3}$，$\sqrt{（-2）^{2}}$=2．
故答案为：2，$\frac{2}{3}$，2．
点评 本题考查了二次根式的性质与化简，解决本题的关键是熟记二次根式的性质．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
相关题目
5．
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）| A． | a+b＞0 | B． | a-b＜0 | C． | ab＞0 | D． | $\frac{a}{b}＜0$ |
12．
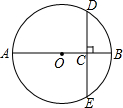如图，⊙O的直径AB=8，弦DE经过OB的中点C且DE⊥OB，则弦DE的长为（ ）
如图，⊙O的直径AB=8，弦DE经过OB的中点C且DE⊥OB，则弦DE的长为（ ）| A． | 3$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
如图，△ABC中，BC的垂直平分线交AB于点D，交BC于点E，若AB=6，AC=4，求△ACD的周长．
6．
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | 3$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
共有5个正三角形，从位置来看，下图中（ ）是由如图平移得到的．
