题目内容
12.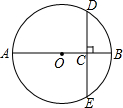 如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )
如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 连接OD,先求出OD及OC的长,再由勾股定理求出DE的长即可.
解答  解:连接OD,
解:连接OD,
∵⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,
∴OD=4,OC=2,DE=2CD.
∵CD=$\sqrt{{OD}^{2}-{OC}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴DE=2CD=4$\sqrt{3}$.
故选:C.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分弦并且平分弦所对的弧是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
4.下列各组式子中,不是同类二次根式的是( )
| A. | $\sqrt{\frac{1}{8}}$和$\sqrt{18}$ | B. | $\sqrt{63}$和$\sqrt{\frac{25}{28}}$ | C. | $\sqrt{48}$和$\sqrt{4.8}$ | D. | $\sqrt{0.125}$和$\sqrt{128}$ |
1.下列说法错误的是( )
| A. | 有两个角互余的三角形一定是直角三角形 | |
| B. | 直角三角形中,若一直角边等于斜边的一半,则这条直角边所对的角为30° | |
| C. | 直角三角形斜边上的中线等于斜边的一半 | |
| D. | △ABC中,若∠A:∠B:∠C=1:3:5,则这个三角形为直角三角形 |
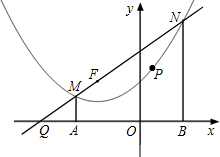 如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.