题目内容
20.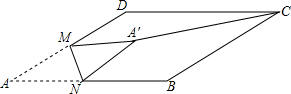 如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3$\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是5.
如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3$\sqrt{3}$,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是5.
分析 如图,作辅助线;首先求出线段ME、DE的长度;运用勾股定理求出MC的长度,即可解决问题.
解答 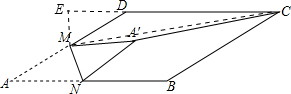 解:如图,连接MC;过点M作ME⊥CD,
解:如图,连接MC;过点M作ME⊥CD,
交CD的延长线于点E;
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=4,
∵点M为AD的中点,∠BCD=30°,
∴DM=MA=2,∠MDE=∠BCD=30°,
∴ME=$\frac{1}{2}$DM=1,DE=$\sqrt{3}$,
∴CE=CD+DE=4$\sqrt{3}$,由勾股定理得:
CM2=ME2+CE2,
∴CM=7;由翻折变换的性质得:MA′=MA=2,
显然,当折线MA′C与线段MC重合时,
线段A′C的长度最短,此时A′C=7-2=5,
故答案为5.
点评 该题以平行四边形为载体,以翻折变换为手段,以考查平行四边形的性质、勾股定理等几何知识点为核心构造而成;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用平行四边形的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
8.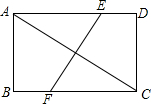 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{8}$ | C. | 15 | D. | 16 |
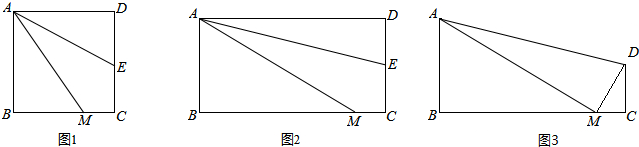
 如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm.
如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm. 如图,已知△ABC,
如图,已知△ABC,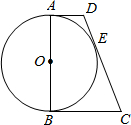 如图,在直角梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O的直径,OA=2,CD与⊙O相切于点E.求CD的长.
如图,在直角梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O的直径,OA=2,CD与⊙O相切于点E.求CD的长.