题目内容
14. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达点B处停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为ts.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达点B处停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为ts.(1)MN与AC的数量关系是MN=$\frac{1}{2}$AC;
(2)求点D由点A向点B匀速运动的过程中,线段MN所扫过区域的面积;
(3)当t为何值时,△DMN是等腰三角形?
分析 (1)直接利用三角形中位线证明即可;
(2)分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,根据题意可得线段MN扫过区域的面积就是?AFGE的面积求解即可;
(3)分三种情况:①当MD=MN=3时,②当MD=DN,③当DN=MN时,分别求解△DMN为等腰三角形即可.
解答 解:(1)∵在△ADC中,M是AD的中点,N是DC的中点,
∴MN=$\frac{1}{2}$AC;
故答案为:MN=$\frac{1}{2}$AC;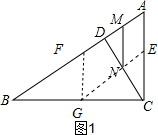 (2)如图1,分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,
(2)如图1,分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,
根据题意可得线段MN扫过区域的面积就是?AFGE的面积,
∵AC=6,BC=8,
∴AE=3,GC=4,
∵∠ACB=90°,
∴S四边形AFGE=AE•GC=3×4=12,
∴线段MN所扫过区域的面积为12.
(3)据题意可知:MD=$\frac{1}{2}$AD,DN=$\frac{1}{2}$DC,MN=$\frac{1}{2}$AC=3,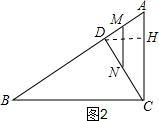 ①当MD=MN=3时,△DMN为等腰三角形,此时AD=AC=6,
①当MD=MN=3时,△DMN为等腰三角形,此时AD=AC=6,
∴t=6,
②当MD=DN时,AD=DC,如图2,过点D作DH⊥AC交AC于H,则AH=$\frac{1}{2}$AC=3,
∵cosA=$\frac{AH}{AD}$=$\frac{AC}{AB}$,
∴$\frac{3}{AD}$=$\frac{6}{10}$,解得AD=5,
∴AD=t=5.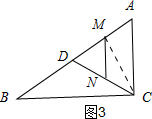 ③如图3,当DN=MN=3时,AC=DC,连接MC,则CM⊥AD,
③如图3,当DN=MN=3时,AC=DC,连接MC,则CM⊥AD,
∵cosA=$\frac{AM}{AC}$=$\frac{AC}{AB}$,即$\frac{AM}{6}$=$\frac{6}{10}$,
∴AM=$\frac{18}{5}$,
∴AD=t=2AM=$\frac{36}{5}$,
综上所述,当t=5或6或$\frac{36}{5}$时,△DMN为等腰三角形.
点评 此题属于三角形的综合题.考查了等腰三角形的性质,平行四边形的面积、三角形中位线以及锐角三角函数的知识.注意掌握辅助线的作法、掌握分类讨论思想的应用是解此题的关键.

| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 80 | 70 |
(1)两个年级参加春游学生人数之和超过200人吗?为什么?
(2)两个年级参加春游学生各有多少人?
| A. | 1-2x=$\frac{10}{11}$ | B. | (1-x)2=$\frac{10}{11}$ | C. | 1-2x=$\frac{9}{10}$ | D. | (1-x)2=$\frac{9}{10}$ |
 在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:EF=EC.
在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:EF=EC. 如图,三条直线两两相交于点O,∠AOE的对顶角是∠BOF,∠AOD的邻补角是∠AOC、∠DOB.
如图,三条直线两两相交于点O,∠AOE的对顶角是∠BOF,∠AOD的邻补角是∠AOC、∠DOB. 如图,在 Rt△ABC中,∠ACB=90°,BC=6,AC=8,AB的垂直平分线 DE交 BC的延长线于F,则 CF的长为$\frac{7}{3}$.
如图,在 Rt△ABC中,∠ACB=90°,BC=6,AC=8,AB的垂直平分线 DE交 BC的延长线于F,则 CF的长为$\frac{7}{3}$. 如图,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数.
如图,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的度数为40°.
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的度数为40°.