题目内容
16.如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上且△ABC折成的“叠加矩形”为正方形.
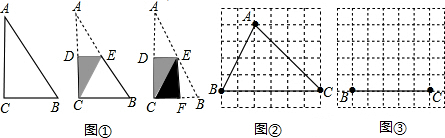
分析 (1)应先在三角形的格点中找一个矩形,折叠即可;
(2)根据正方形的边长应等于底边及底边上高的一半可得所求三角形的底边与高相等.
解答 解:(1)如图②所示:
(2)如图③所示:
点评 本题主要考查作图-轴对称变换,解决本题的关键是得到相应矩形的边长等于所给三角形的底边与底边上的高的一半的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.等腰三角形的一个外角为60°,则它的顶角的度数为( )
| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
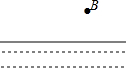 如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)
如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)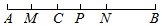 如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.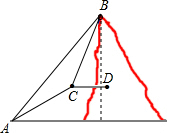 如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?
如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?