题目内容
16.已知反比例函数的图象经过点A(1,-2),过反比例函数图象上一点M作MN⊥x轴于点N,连接OM,求△MON的面积.分析 首先利用待定系数法求得反比例函数的解析式,先设M的坐标是(a,b),由于点M在函数图象上,那么b=$\frac{k}{a}$,即ab=k=-2,进而据图可求△MON的面积.
解答  解:设反比例函数的解析式是y=$\frac{k}{x}$,
解:设反比例函数的解析式是y=$\frac{k}{x}$,
把(1,-2)代入y=$\frac{k}{x}$,得k=-2,则函数解析式是y=-$\frac{2}{x}$.
如右图,设M的坐标是(a,b),那么
b=-$\frac{2}{a}$,
∴ab=k=-2,
∴S△MON=$\frac{1}{2}$ON•MN=$\frac{1}{2}$×|ab|=$\frac{1}{2}$×2=1.
点评 本题考查了反比例函数系数k的几何意义,解题的关键是注意反比例函数图象上点的横纵坐标之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知(-1.2,y1),(-0.5,y2),(2.9,y3)是直线y=-5x+a(a为常数)上的三个点,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
11.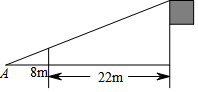 如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
 如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )| A. | 6m | B. | 8.8m | C. | 12m | D. | 30m |
1.某超市货架上摆放着桶装方便面,如图是它们的三视图,则货架上的桶装方便面至少有( )


| A. | 8桶 | B. | 9桶 | C. | 10桶 | D. | 11桶 |
8.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.下列汽车标志的图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 已知实数a,b,c在数轴上的位置如图,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值.
已知实数a,b,c在数轴上的位置如图,求式子|c-b|-|-b|+$\sqrt{{a}^{2}}$+|a+c|的值.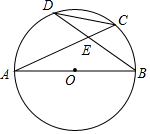 如图所示,AB是⊙O的直径,弦AC、BD相交于点E,且C为弧BD的中点.若EC=2,tan∠CEB=2.
如图所示,AB是⊙O的直径,弦AC、BD相交于点E,且C为弧BD的中点.若EC=2,tan∠CEB=2.