题目内容
 已知平行四边形ABCD(如图),点P在边AB上,且AP:PD=1:2,点Q是CD的中点,如果设
已知平行四边形ABCD(如图),点P在边AB上,且AP:PD=1:2,点Q是CD的中点,如果设| AB |
| a |
| AD |
| b |
| PQ |
考点:*平面向量
专题:
分析:表示出
、
,然后根据向量的三角形法则解答即可.
| PD |
| DQ |
解答:解:∵AP:PD=1:2,
=
,
∴
=
=
,
∵点Q是CD的中点,
∴
=
=
,
∴
=
+
=
+
.
故答案为:
+
.
| AD |
| b |
∴
| PD |
| 2 |
| 1+2 |
| AD |
| 2 |
| 3 |
| b |
∵点Q是CD的中点,
∴
| DQ |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| a |
∴
| PQ |
| PD |
| DQ |
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| b |
故答案为:
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| b |
点评:本题考查了平面向量,平面向量的问题,熟练掌握平行四边形法则和三角形法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
下列命题中正确的共有( )个
①向量
与
是平行向量,则A、B、C、D四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形必须
=
;
⑤模为0的向量方向不确定.
①向量
| AB |
| CD |
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形必须
| AB |
| DC |
⑤模为0的向量方向不确定.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法中正确的是( )
| A、无限小数都是无理数 |
| B、数轴上的点都表示有理数 |
| C、平方根等于它本身的是1和0 |
| D、立方根等于它本身的是-1、0和1 |
下列命题错误的是( )
| A、经过三个点一定可以作圆 |
| B、三角形的外心到三角形各顶点的距离相等 |
| C、同圆或等圆中,相等的圆心角所对的弧相等 |
| D、平分弦(不是直径)的直径垂直于弦 |
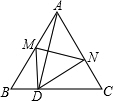 如图,等边△ABC边长为a,D是BC边上一点,且BD:DC=2:3,把△ABC折叠,使A落在BC边上的D处.
如图,等边△ABC边长为a,D是BC边上一点,且BD:DC=2:3,把△ABC折叠,使A落在BC边上的D处.