题目内容
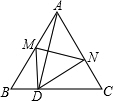如图，等边△ABC边长为a，D是BC边上一点，且BD：DC=2：3，把△ABC折叠，使A落在BC边上的D处．（1）设折痕为MN，求
| AM |
| AN |
（2）如果
| BD |
| DC |
| m |
| n |
| AM |
| AN |
考点：翻折变换（折叠问题）,相似三角形的判定与性质
专题：
分析：（1）设出未知数，运用余弦定理列出关于线段AM的方程，求出AM的长度；同理求出线段AN的长度，即可解决问题．（2）类比（1）中的解法，同理可求出AM、AN的长度，即可解决问题．
解答：解：（1）由题意得：
AM=DM（设为λ），AN=DN（设为μ），
则BM=a-λ，CN=a-μ；
∵BD：DC=2：3，
∴BD=
a，DC=
a；
∵△ABC为等边三角形，
∴∠B=∠C=60°；
在△BDM中，由余弦定理得：
λ2=(a-λ)2+(
a)2-2×
a(a-λ)cos60°，
化简整理得：λ=
a；
在△DCN中，同理可求：μ=
∴
=
即
=
（2）
∵
=
，BC=a，
∴BD=
，DC=
；
设AM=DM=λ，AN=DN=μ，
则BM=a-λ，CN=a-μ；
类比（1）中的方法，根据余弦定理列出方程，
可求得：λ=
，μ=
，
∴
=
，
即
=
．
解：（1）由题意得：AM=DM（设为λ），AN=DN（设为μ），
则BM=a-λ，CN=a-μ；
∵BD：DC=2：3，
∴BD=
| 2 |
| 5 |
| 3 |
| 5 |
∵△ABC为等边三角形，
∴∠B=∠C=60°；
在△BDM中，由余弦定理得：
λ2=(a-λ)2+(
| 2 |
| 5 |
| 2 |
| 5 |
化简整理得：λ=
| 19 |
| 40 |
在△DCN中，同理可求：μ=
| 19a |
| 35 |
∴
| λ |
| μ |
| 7 |
| 8 |
即
| AM |
| AN |
| 7 |
| 8 |
（2）
∵
| BD |
| DC |
| m |
| n |
∴BD=
| ma |
| m+n |
| na |
| m+n |
设AM=DM=λ，AN=DN=μ，
则BM=a-λ，CN=a-μ；
类比（1）中的方法，根据余弦定理列出方程，
可求得：λ=
| a(m2+mn+n2) |
| (m+2n)(m+n) |
| a(m2+mn+n2) |
| (2m+n)(m+n) |
∴
| λ |
| μ |
| 2m+n |
| m+2n |
即
| AM |
| AN |
| 2m+n |
| m+2n |
点评：该题以等边三角形形为载体，以翻折变换为方法，以考查翻折变换的性质、余弦定理及其应用等知识点为核心构造而成；解题的关键是灵活运用有关定理来分析、解答；对求解运算能力提出了较高的要求．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图，在△ABC中，D是AB的中点，DE∥BC，若△ADE的面积为3，则△ABC的面积为（ ）| A、3 | B、6 | C、9 | D、12 |
数轴上的点所表示的数一定是（ ）
| A、整数和分数 |
| B、有理数和分数 |
| C、有理数和无理数 |
| D、整数和无理数 |
已知平行四边形ABCD（如图），点P在边AB上，且AP：PD=1：2，点Q是CD的中点，如果设
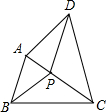如图，四边形ABCD中，∠A、∠B、∠C、∠D的角平分线恰相交于一点P，记△APD、△APB、△BPC、△DPC的面积分别为S1、S2、S3、S4，则有（ ）| A、S1+S3=S2+S4 |
| B、S1+S2=S3+S4 |
| C、S1+S4=S2+S3 |
| D、S1=S3 |
如图所示的几何体中，面与面相交形成的线共有