题目内容
已知线段AB=6cm,在直线AB上截取线段BC=4cm,若M,N分别是AB,BC的中点.
(1)求M,N间的距离;
(2)若AB=acm,BC=bcm,其它条件不变,此时M,N间的距离是多少?
(3)分析(1)(2)的解答过程,从中你发现了什么规律?在同伴间交流你得到的启迪.
(1)求M,N间的距离;
(2)若AB=acm,BC=bcm,其它条件不变,此时M,N间的距离是多少?
(3)分析(1)(2)的解答过程,从中你发现了什么规律?在同伴间交流你得到的启迪.
考点:两点间的距离
专题:
分析:(1)根据题意画出图形,由M,N分别是AB,BC的中点求出MC及NC的长.根据MN=MC+NC即可得出结论;
(2)根据由M,N分别是AB,BC的中点用a,b表示出出MC及NC的长,进而可得出结论;
(3)由(1)、(2)的规律即可得出结论.
(2)根据由M,N分别是AB,BC的中点用a,b表示出出MC及NC的长,进而可得出结论;
(3)由(1)、(2)的规律即可得出结论.
解答: 解:(1)如图所示,
解:(1)如图所示,
∵线段AB=6cm,线段BC=4cm,
∴AC=AB-BC=6-4=2cm.
∵M,N分别是AB,BC的中点,
∴MC=
AC=1(cm),NC=
BC=2(cm),
∴MN=MC+NC=1+2=3(cm).
答:M,N间的距离是3cm;
(2)∵AB=acm,BC=bcm,
∴AC=AB-BC=(a-b)=2cm.
∵M,N分别是AB,BC的中点,
∴MC=
AC=
(a-b)cm,NC=
BC=
b(cm),
∴MN=MC+NC=
(a-b)+
b=
a(cm).
答:M,N间的距离是
acm;
(3)由(1)(2)可得,无论线段AB为何值,MN=
AB.
 解:(1)如图所示,
解:(1)如图所示,∵线段AB=6cm,线段BC=4cm,
∴AC=AB-BC=6-4=2cm.
∵M,N分别是AB,BC的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NC=1+2=3(cm).
答:M,N间的距离是3cm;
(2)∵AB=acm,BC=bcm,
∴AC=AB-BC=(a-b)=2cm.
∵M,N分别是AB,BC的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:M,N间的距离是
| 1 |
| 2 |
(3)由(1)(2)可得,无论线段AB为何值,MN=
| 1 |
| 2 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,D是AB的中点,DE∥BC,若△ADE的面积为3,则△ABC的面积为( )
如图,在△ABC中,D是AB的中点,DE∥BC,若△ADE的面积为3,则△ABC的面积为( )| A、3 | B、6 | C、9 | D、12 |
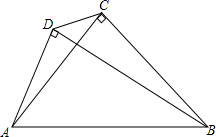 △ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系.
△ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系. 已知平行四边形ABCD(如图),点P在边AB上,且AP:PD=1:2,点Q是CD的中点,如果设
已知平行四边形ABCD(如图),点P在边AB上,且AP:PD=1:2,点Q是CD的中点,如果设