题目内容
在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=10:20:30,③∠A=90°-∠B,④∠A=2∠B=3∠C,能确定△ABC是直角三角形的条件有 .(只填序号,多填、填错或不填不给分,少填的酌情给分)
考点:三角形内角和定理
专题:
分析:根据①②③④分别证明∠C=90°,即可证明△ABC是直角三角形,即可解题.
解答:解:①∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°∴①正确;
②∵∠A:∠B:∠C=10:20:30,∠A+∠B+∠C=180°,∴∠C=90°,∴②正确;
③∵∠A=90°-∠B,∠A+∠B+∠C=180°,∴∠C=90°,∴③正确;
④∵∠A=2∠B=3∠C,∠A+∠B+∠C=180°,∴∠C=90°,∴④正确.
故答案为①②③④.
②∵∠A:∠B:∠C=10:20:30,∠A+∠B+∠C=180°,∴∠C=90°,∴②正确;
③∵∠A=90°-∠B,∠A+∠B+∠C=180°,∴∠C=90°,∴③正确;
④∵∠A=2∠B=3∠C,∠A+∠B+∠C=180°,∴∠C=90°,∴④正确.
故答案为①②③④.
点评:本题考查了三角形内角和为180°的性质,本题中求∠C=90°是解题的关键.

练习册系列答案
相关题目
一条弧所对的圆心角是90°,半径为1,则这条弧的长度是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
代数式6x2y+
,4xy+y2,
x+y,
,-2,a中,不是整式的有( )
| 1 |
| x |
| 1 |
| 3 |
| 2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
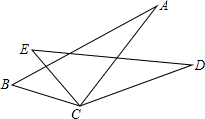 如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )
如图,从下列:①BC=EC,②AC=DC,③AB=DE,④∠ACD=∠BCE中任取三个为条件,余下的一个为结论,则最多可以构成正确说法的个数是( )
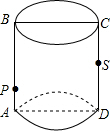 如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是
如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是