Question

19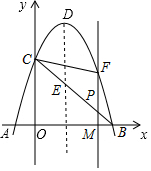．如图，抛物线y=-x²+2x+3与x轴相交于A、B两点，与y轴相交于点C，顶点为D．
（1）直接写出A，B，C三点的坐标：A（-1，0）；B（3，0）；C（0，3）
（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF⊥x轴于点M，交抛物线于点F．设点P的横坐标为m：
①用含m的代数式表示线段PF的长；
②当m为何值时，四边形PEDF为平行四边形？

Answer 1

分析 （1）对于抛物线解析式，令x=0求出y的值，确定出OC的值，得出C的坐标，令y=0求出x的值，确定出A，B的坐标，进而得出抛物线对称轴；
（2）①设直线BC的解析式为y=kx+b，将B与C坐标代入求出k与b的值，即可确定出直线BC解析式；将x=1代入抛物线解析式，求出y的值，确定出D坐标，将x=1代入直线BC解析式求出y的值，确定出E坐标，求出DE长，将x=m代入抛物线解析式表示出F纵坐标，将x=m代入直线BC解析式表示出P纵坐标，两纵坐标相减表示出线段PF，
②由DE与FP平行，要使四边形PEDF为平行四边形，只需DE=PF，列出关于m的方程，求出方程的解得到m的值，检验即可．

解答 解：（1）在y=-x²+2x+3中，当x=0时，y=3，
∴C（0，3），
当y=0时，-x²+2x+3=0，
解：得x₁=-1或x₂=3，
∴A（-1，0），B（3，0），
故答案为：-1，0；3，0；0，3；

（2）①设直线BC的函数关系式为：y=kx+b．
把B（3，0），C（0，3）分别代入得：$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$，
解得：k=-1，b=3，
∴直线BC的函数关系式为：y=-x+3；
在y=-x²+2x+3中，当x=1时，y=4，
∴D（1，4），
当x=1时，y=-1+3=2，
∴E（1，2）．
当x=m时，y=-m+3，
∴P（m，-m+3）．
当x=m时，y=-m²+2m+3，
∴F（m，-m²+2m+3），
∴线段DE=4-2=2，
∴线段PF=-m²+2m+3-（-m+3）=-m²+3m，
②∵PF∥DE，
∴当PF=ED时，四边形PEDF为平行四边形，
由-m²+3m=2，解得：m=2或m=1（不合题意，舍去）．
则当m=2时，四边形PEDF为平行四边形．

点评 此题考查了二次函数综合题，涉及的知识有：坐标与图形性质，一次函数与坐标轴的交点，抛物线与坐标轴的交点，平行四边形的判定，以及待定系数法求函数解析式，熟练掌握待定系数法是解本题第二问的关键．