题目内容
1.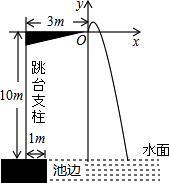 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.
如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为10$\frac{2}{3}$米.
分析 直接利用配方法得出二次函数的最值,进而得出运动员在空中运动的最大高度离水面的距离.
解答 解:∵y=-$\frac{25}{6}$x2+$\frac{10}{3}$x
=-$\frac{25}{6}$(x2-$\frac{4}{5}$x)
=-$\frac{25}{6}$(x-$\frac{2}{5}$)2+$\frac{2}{3}$,
∴y的最大值为:$\frac{2}{3}$,
∴运动员在空中运动的最大高度离水面为:10+$\frac{2}{3}$=10$\frac{2}{3}$(m).
故答案为:10$\frac{2}{3}$.
点评 此题主要考查了二次函数的应用,正确得出二次函数最值是解题关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
10.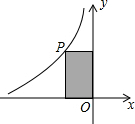 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
 如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.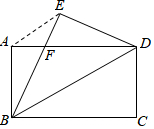 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.证明:
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.证明: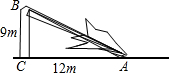 如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.
如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.