题目内容

在数学中，为了简便，记
n
k=1
k=1+2+3+…+(n-1)+n．1!=1，2!=2×1，3!=2×2×1，…，n!=n×（n-1）×（n-2）×…×2×1．则
2011
k=1
k-
2012
k=1
k+
2012!
2011!
=（　　）
A、2011B、-1
C、0D、2012
考点：有理数的混合运算
专题：新定义
分析：原式利用题中的新定义化简，计算即可得到结果．
解答： 解：根据题中的新定义得：原式=1+2+…+2011-1-2-…-2011-2012+2012=0．
故选C
点评：此题考查了有理数的混合运算，弄清题中的新定义是解本题的关键．
练习册系列答案
相关题目
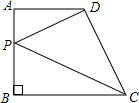如图，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AD=1，AB=3，BC=3，点P是AB上一个动点，则PC+PD的和最小值为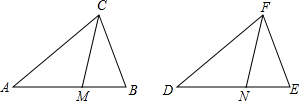
 
．
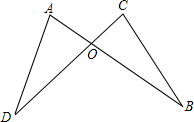若|x-1|+（y-2）2+
z-3
=0，则x+y+z的值为（　　）
A、6B、5C、4D、3
某学习小组学习了全等三角形的判定和性质以后，想运用全等三角形的知识去研究下面的问题：
【问题提出】如图1，在△ABC和△DEF中，∠A=∠D，∠B=∠E，CM、FN分别是△ABC和△DEF的角平分线，且CM=FN，试证明△ABC≌△DEF．
【问题思考】如图2，在△ABC和△DEF中，AC=DF，BC=EF，CM、FN分别是△ABC和△DEF的中线，且CM=FN，试探究∠B与∠E的关系，请写出你的结论：
 
（不要求证明）
【深入研究】小组同学进一步探究，若把问题2变为：在△ABC和△DEF中，AC=DF，BC=EF，CM、FN分别是△ABC和△DEF的高，且CM=FN，试探究∠B=∠E的关系，请写出你的结论：
 
（不要求证明）．
已知，如图，AB，CD相交于点O，且AB=CD，AD=CB．试说明OB=OD．
如图，AB=AD，BC=DC，∠1=35°，则∠BCD是多少度？
下列语句中不是命题的有（　　）
（1）两点之间，线段最短；（2）不许大声讲话；（3）连接A、B两点；（4）鸟是动物；（5）不相交的两条直线叫做平行线；（6）无论a为怎样的有理数，式子a2+1的值都是正数吗？
A、2个B、3个C、4个D、5个
如图，已知∠C=∠AOC，OC平分∠AOD，OC⊥OE，∠C=63°，求∠D、∠BOE的度数．
计算：（x+1）（x2-x+1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网