题目内容
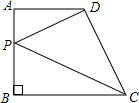 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=1,AB=3,BC=3,点P是AB上一个动点,则PC+PD的和最小值为
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=1,AB=3,BC=3,点P是AB上一个动点,则PC+PD的和最小值为考点:轴对称-最短路线问题
专题:
分析:要求PC+PD的和的最小值,PC,PD不能直接求,可考虑通过作辅助线转化PC,PD的值,从而找出其最小值求解.
解答:
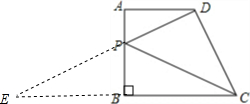 解:延长CB到E,使EB=CB=3,连接DE交AB于P.则DE就是PC+PD的和的最小值.
解:延长CB到E,使EB=CB=3,连接DE交AB于P.则DE就是PC+PD的和的最小值.
∵AD∥BE,
∴∠A=∠PBE,∠ADP=∠E,
∴△ADP∽△BEP,
∴AP:BP=AD:BE=1:3,
∴PB=3AP,
∵AP+BP=AB=3,
∴AP=
,BP=
,
∴PD=
=
,PE=
=
,
∴DE=PD+PE=5,
∴PC+PD的最小值是5,
故答案为:5.
 解:延长CB到E,使EB=CB=3,连接DE交AB于P.则DE就是PC+PD的和的最小值.
解:延长CB到E,使EB=CB=3,连接DE交AB于P.则DE就是PC+PD的和的最小值.∵AD∥BE,
∴∠A=∠PBE,∠ADP=∠E,
∴△ADP∽△BEP,
∴AP:BP=AD:BE=1:3,
∴PB=3AP,
∵AP+BP=AB=3,
∴AP=
| 3 |
| 4 |
| 9 |
| 4 |
∴PD=
| PA2+AD2 |
| 5 |
| 4 |
| PB2+BE2 |
| 15 |
| 4 |
∴DE=PD+PE=5,
∴PC+PD的最小值是5,
故答案为:5.
点评:此题考查了轴对称的性质、勾股定理的运用及相似三角形的判定和性质,解题时要注意找到对称点,并根据“两点之间线段最短”确定P点的位置.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一组数据10,9,7,8,9,11的众数是( )
| A、10 | B、7 | C、9 | D、8 |
下列运算错误的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
一组数据3,-2,8,3,x的极差是10,那么x的取值有( )
| A、1个 | B、2个 | C、3个 | D、无数个 |
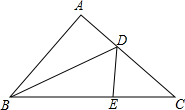 如图,在△ABC中,AB=AC,BD平分∠ABC,E为BC上一点,∠A与∠DEC为一对互补角,若BC=11cm,则△DEC的周长为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,E为BC上一点,∠A与∠DEC为一对互补角,若BC=11cm,则△DEC的周长为( )| A、10cm | B、11cm |
| C、12cm | D、13cm |
 如图,在正方形ABCD中,点E是AB的中点,在AC上确定一点P,使PE+PB最短,请在图上画出点P的位置(保留作图痕迹).
如图,在正方形ABCD中,点E是AB的中点,在AC上确定一点P,使PE+PB最短,请在图上画出点P的位置(保留作图痕迹).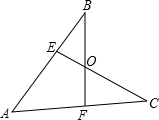 如图,已知E,F分别在AB,AC上,且AE=AF,AB=AC,∠A=60°,∠B=24°,求∠BOE的度数.
如图,已知E,F分别在AB,AC上,且AE=AF,AB=AC,∠A=60°,∠B=24°,求∠BOE的度数.