题目内容
9.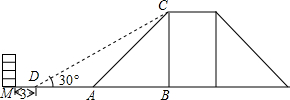 如图是某市一座人行过街天桥,天桥高CB=5米,斜坡AC的坡度为1:1,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的傾斜角为30°.若新坡脚前需留3m的人行道,问离原坡脚A处7m的建筑物M是否需要拆除,请说明理由.($\sqrt{3}$≈1.73)
如图是某市一座人行过街天桥,天桥高CB=5米,斜坡AC的坡度为1:1,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的傾斜角为30°.若新坡脚前需留3m的人行道,问离原坡脚A处7m的建筑物M是否需要拆除,请说明理由.($\sqrt{3}$≈1.73)
分析 根据斜坡AC的坡度为1:1,求出AB的长,根据新坡面的傾斜角为30°,求出BD的长,计算比较得到答案.
解答 解:在Rt△ABC中,∠ABC=90°,BC=5,
∵i=1:1,∴AB=5,
在Rt△DBC中,∠DBC=90°,∠CDB=30°,BC=5,
tan30°=$\frac{BC}{DB}$,
∴$\frac{BC}{DB}$=$\frac{\sqrt{3}}{3}$,
解得DB=$5\sqrt{3}$=5×1.73≈8.65,
∵BM=7+5=12,BD≈8.65,
∴12-8.65>3,
所以,离原坡脚7m的建筑物无需拆除.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念,选择合适的三角函数是解题的关键.

练习册系列答案
相关题目
19. 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
 在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )
在平行四边形ABCD中,若∠A=30°,AB边上的高为8,则BC的长为( )| A. | 16 | B. | 8 | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
20.随着综艺节目“爸爸去哪儿”的热播,问卷调查公司为调查了解该节目在中学生中受欢迎的程度,走进某校园随机抽取部分学生就“你是否喜欢看爸爸去哪儿”进行问卷调查,并将调查结果统计后绘制成如下不完整的统计表:
则a-b=0.1.
| 非常喜欢 | 喜欢 | 一般 | 不知道 | |
| 频数 | 200 | 30 | 10 | |
| 频率 | a | b | 0.025 |
1.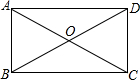 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 8 |
19.一个等腰三角形的一边长是6,另一边长是8.那么这个等腰三角形的周长是( )
| A. | 20 | B. | 20或24 | C. | 22 | D. | 20或22. |
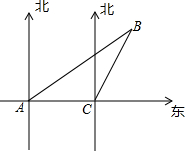 三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)
三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)
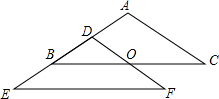 如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.
如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.