题目内容
2.观察下列各式:∵$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,$\frac{1}{2012×2013}$=$\frac{1}{2012}$-$\frac{1}{2013}$.
∴$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2012×2013}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$=1-$\frac{1}{2013}$=$\frac{2012}{2013}$
根据观察,则方程$\frac{1}{x(x+2)}$+$\frac{1}{(x+2)(x+4)}$+…+$\frac{1}{(x+8)(x+10)}$=$\frac{5}{24}$的解为x1=2,x2=-12.
分析 已知方程利用拆项法变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:已知方程整理得:$\frac{1}{2}$($\frac{1}{x}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+4}$+…+$\frac{1}{x+8}$-$\frac{1}{x+10}$)=$\frac{5}{24}$,
即$\frac{1}{x}$-$\frac{1}{x+10}$=$\frac{5}{12}$,
去分母得:12x+120-12x=5x2+50x,即x2+10x-24=0,
分解因式得:(x-2)(x+12)=0,
解得:x1=2,x2=-12,
经检验x1=2,x2=-12都为分式方程的解.
故答案为:x1=2,x2=-12
点评 此题考查了分式方程的解,解题的关键是将已知方程利用拆项法变形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
16.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$,则2xy的值是( )
| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
17. “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
 如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.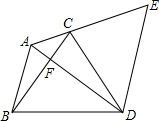 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.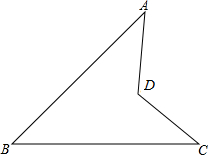 如图,三个内角∠A、∠B、∠C均为45°.
如图,三个内角∠A、∠B、∠C均为45°.