题目内容
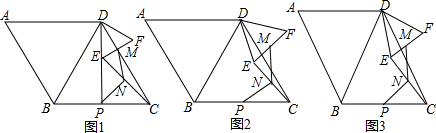
12.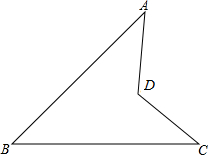 如图,三个内角∠A、∠B、∠C均为45°.
如图,三个内角∠A、∠B、∠C均为45°.(1)求证:CD⊥AB;
(2)连接BD和AC,判断BD和AC的关系,并证明.
分析 (1)延长CD与AB交与点E,由∠B、∠C均为45°,利用三角形的内角和定理可知∠BEC=90°,得CD⊥AB;
(2)延长BD与AC交于点F,首先证明Rt△AEC≌Rt△DEB,由全等三角形的性质易得BD=AC,∠EBD=∠ECA,易得∠BED=∠CFD=90°,得出结论.
解答 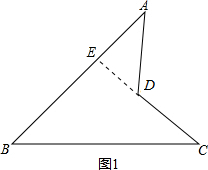 解:(1)如图1,延长CD与AB交与点E,
解:(1)如图1,延长CD与AB交与点E,
∵∠B=∠C=45°,
∴∠BEC=90°,
∴CD⊥AB;
(2)BD=AC且BD⊥AC.
延长BD与AC交于点F,
∵∠CED=∠AED=90°,∠BAD=45°,
∴∠ADE=45°,
∴AE=DE,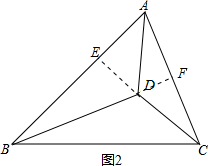
∵∠ABC=∠BCE=45°,
∴BE=CE,
在Rt△AEC与Rt△DEB中,
$\left\{\begin{array}{l}{AE=DE}\\{∠AED=∠DEB}\\{CE=BE}\end{array}\right.$,
∴Rt△AEC≌Rt△DEB,
∴BD=AC,∠EBD=∠ECA,
∵∠BDE=∠CDF,
∴∠BED=∠CFD=90°,
∴BD⊥AC,
∴BD=AC且BD⊥AC.
点评 本题主要考查了垂直的定义,等腰直角三角形的性质,全等三角形的性质及判定定理,作出适当的辅助线,证明三角形全等是解答此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
2.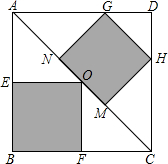 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )| A. | $\frac{19}{36}$ | B. | $\frac{1}{2}$ | C. | $\frac{17}{36}$ | D. | $\frac{17}{32}$ |
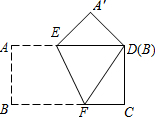 把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.
把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.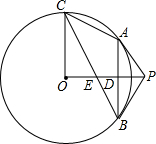 如图所示,已知P为⊙O外一点,PA为⊙O的切线,A为切点,B为⊙O上一点,且PA=PB,连接OP、AB相交于点D,过点O作OC⊥OP交⊙O于C,连接BC交OP于E.
如图所示,已知P为⊙O外一点,PA为⊙O的切线,A为切点,B为⊙O上一点,且PA=PB,连接OP、AB相交于点D,过点O作OC⊥OP交⊙O于C,连接BC交OP于E.