题目内容
9．⊙O中，若弦AB长2$\sqrt{2}$cm，圆心到此弦的距离为$\sqrt{2}$cm，则此弦所对的圆周角等于45°或135°．分析 首先根据题意画出图形，然后由垂径定理，求得AC的长，即可得△OAC是等腰直角三角形，则可求得∠AOB的度数，然后由圆周角定理，求得答案．
解答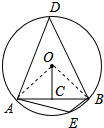 
解：如图，连接OA，OB，则AB=2$\sqrt{2}$cm，OC=$\sqrt{2}$cm，
∵OC⊥AB，
∴AC=$\frac{1}{2}$AB=$\sqrt{2}$（cm），
∴OC=AC，
∴∠AOC=45°，
∴∠AOB=90°，
∴∠ADB=$\frac{1}{2}$∠AOB=45°，
∴∠AEB=180°-∠ADB=135°．
∴此弦所对的圆周角等于45°或135°．
故答案为45°或135°．
点评 本题考查了圆周角定理、垂径定理、等腰直角三角形的性质以及圆的内接四边形的性质．此题难度适中，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
相关题目
20．
如图所示，△ABC∽△ACD，且AB=10cm，AC=8cm，则AD的长是（ ）
如图所示，△ABC∽△ACD，且AB=10cm，AC=8cm，则AD的长是（ ）| A． | 6.4cm | B． | 6cm | C． | 2cm | D． | 4cm |
17．
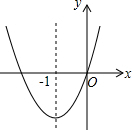如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=-1，下列结论中：?①ab＞0，?②a+b+c＞0，?③当-2＜x＜0时，y＜0，④2a-b=0，正确的个数是（ ）
如图，已知经过原点的抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=-1，下列结论中：?①ab＞0，?②a+b+c＞0，?③当-2＜x＜0时，y＜0，④2a-b=0，正确的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3 个 | D． | 4个 |
4．观察下列等式：
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
| A． | $\frac{1}{2}-\frac{1}{{21×{2^{21}}}}$ | B． | $\frac{1}{2}-\frac{1}{{22×{2^{22}}}}$ | C． | $\frac{1}{2}-\frac{1}{{23×{2^{23}}}}$ | D． | $\frac{1}{2}-\frac{1}{{24×{2^{24}}}}$ |