题目内容
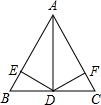如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，则下列四个结论中：①DE=DF； ②AD上任意一点到AB、AC的距离相等； ③∠BDE=∠CDF；④BD=CD，AD⊥BC．其中正确的有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：等腰三角形的性质,角平分线的性质
专题：
分析：由题意知，△ABC是等腰三角形，由三线合一的性质知，点D是BC的中点，AD⊥BC，可得④正确；根据角平分线的性质可得①②正确；再由∠DEB=∠DFC=90°，∠B=∠C，根据三角形内角和定理可得③正确；故可得到4个结论均正确．
解答：解：∵AB=AC，
∴△ABC是等腰三角形，∠B=∠C．
∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，
∴AD⊥BC，BD=CD，DE=DF，AD上任意一点到AB、AC的距离相等，故①②④正确；
∵DE⊥AB于E，DF⊥AC，
∴∠DEB=∠DFC=90°．
∵∠DEB=∠DFC=90°，∠B=∠C，
∴∠BDE=∠CDF，即③正确；
故选D．
∴△ABC是等腰三角形，∠B=∠C．
∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，
∴AD⊥BC，BD=CD，DE=DF，AD上任意一点到AB、AC的距离相等，故①②④正确；
∵DE⊥AB于E，DF⊥AC，
∴∠DEB=∠DFC=90°．
∵∠DEB=∠DFC=90°，∠B=∠C，
∴∠BDE=∠CDF，即③正确；
故选D．
点评：本题考查了等腰三角形的性质，角平分线的性质．做题时要注意思路：由已知结合性质与图形进行思考，由易到难，步步深入．
练习册系列答案
相关题目