题目内容
1.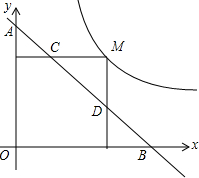 如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.
如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.
分析 作CE⊥x轴于E,DF⊥y轴于F,由直线的解析式为y=-x+m,易得A(0,m),B(m,0),得到△OAB等腰直角三角形,则△ADF和△CEB都是等腰直角三角形,设M的坐标为(a,b),则ab=$\sqrt{3}$,并且CE=b,DF=a,则AD=$\sqrt{2}$DF=$\sqrt{2}$a,BC=$\sqrt{2}$CE=$\sqrt{2}$b,于是得到AD•BC=2ab=2$\sqrt{3}$.
解答 解:∵反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),
∴k=1×$\sqrt{3}$=$\sqrt{3}$,
作CE⊥x轴于E,DF⊥y轴于F,如图,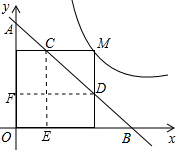
对于y=-x+m,
令x=0,则y=m;令y=0,-x+m=0,解得x=m,
∴A(0,m),B(m,0),
∴△OAB等腰直角三角形,
∴△ADF和△CEB都是等腰直角三角形,
设M的坐标为(a,b),则ab=$\sqrt{3}$,
CE=b,DF=a,
∴AD=$\sqrt{2}$DF=$\sqrt{2}$a,BC=$\sqrt{2}$CE=$\sqrt{2}$b,
∴AD•BC=$\sqrt{2}$a$•\sqrt{2}$b=2ab=2$\sqrt{3}$.
故答案为$\sqrt{3}$,2$\sqrt{3}$.
点评 本题考查了反比例函数综合题:点在反比例函数图象上,点的横纵坐标满足其解析式;会求一次函数与坐标轴的交点坐标以及灵活运用等腰直角三角形的性质.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.在△ABC和△DEF中,按照下列给出的条件,能用“SAS”公理判定△ABC≌△DEF的是( )
| A. | AB=DE,∠A=∠D,BC=EF | B. | AB=EF,∠A=∠D,AC=DF | ||
| C. | AB=BC,∠B=∠E,DE=EF | D. | BC=EF,∠C=∠F,AC=DF |
12.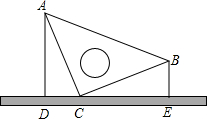 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )| A. | $5\sqrt{3}$厘米 | B. | $5\sqrt{2}$厘米 | C. | 8厘米 | D. | 6厘米 |
16.已知⊙O1与⊙O2的半径分别为2和4,圆心距O1O2=6,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
13.若a、b、c是三个不同的有理数,且a+b+c=0,则下列说法正确的是( )
| A. | 三个数中一定有一个是0 | |
| B. | 三个数若都不为0,则不可能符号都相间 | |
| C. | 一定有两个数互为相反数 | |
| D. | 一定有两个数的和等于第三个数 |
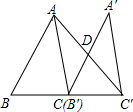 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.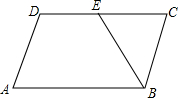 如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2.
如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2.