题目内容
12.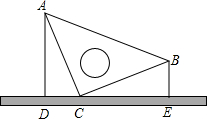 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )| A. | $5\sqrt{3}$厘米 | B. | $5\sqrt{2}$厘米 | C. | 8厘米 | D. | 6厘米 |
分析 根据题意结合全等三角形的判定方法得出△ACD≌△CBE(AAS),进而求出AD=EC,再利用勾股定理得出答案.
解答 解:由题意可得:∠ACD+∠DAC=90°,∠BCE+∠ACD=90°,AC=BC,
则∠DAC=∠BCE,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠CDA=∠BEC}\\{∠DAC=∠ECB}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS),
∴AD=EC,
∵BC=10cm,BE=5cm,
∴AD=EC=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$(cm).
故选:A.
点评 此题主要考查了全等三角形的应用,根据题意得出△ACD≌△CBE是解题关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
3.下列调查中,最适合采用抽样调查的是( )
| A. | 对旅客上飞机前的安检 | B. | 了解全班同学每周体育锻炼的时间 | ||
| C. | 企业招聘,对应聘人员的面试 | D. | 了解某批次灯泡的使用寿命情况 |
7.下列各式中,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{12}-\sqrt{3}=3$ | C. | $\sqrt{2}×\sqrt{3}=\sqrt{5}$ | D. | $\sqrt{12}÷\sqrt{3}=2$ |
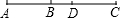 如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.
如图,已知线段AB=6延长线段AB到C,使BC=2AB,点D是AC的中点,则BD=3.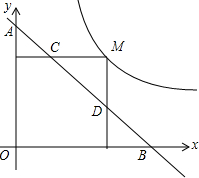 如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.
如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.