题目内容
3.直线l垂直x轴于点A(4,0),点P是直线l上的一个动点,经过点P的抛物线y=x2+bx与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,设P点的纵坐标为m.(1)求当点P与点A重合时抛物线的解析式;
(2)平移直线OP,使平移后的直线与抛物线有且只有一个公共点Q,试证明:无论m为何值时,△OPQ的面积恒为定值,请说明理由并求其值;
(3)连接BC,试问:是否存在点P,使得△PBC为直角三角形?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由.

分析 (1)将点A的坐标代入抛物线的解析式求出b即可得到当点P与点A重合时,抛物线的解析式;、
(2)先得到直线OP的解析式为y=$\frac{m}{4}$x,再用m表示抛物线解析式为y=x2+$\frac{m-16}{4}$x,设直线OP平移后的解析式为y=$\frac{m}{4}$x+n,根据抛物线与直线有且只有一个公共点,得到方程x2+$\frac{m-16}{4}$x=$\frac{m}{4}$x+n有两个相等的实数解,利于判别式的意义可计算出n=4,方程的解为x1=x2=2,则Q(2,$\frac{1}{2}$m-4),作QE∥y轴交OP于E点,则E(2,$\frac{1}{2}$m),然后根据三角形面积公式好,利用S△OPQ=S△OQE+S△PQE进行计算,即可得到无论m为何值时,△OPQ的面积恒为定值8;
(3)分类讨论:当点P在x轴的上方时和当点P在x轴的下方时两种情况利用△PAB∽△PAP得到比例式,从而求得点P的坐标.
解答 (1)解:把A(4,0)代入抛物线解析式,可得0=42+4b,
解得b=-4,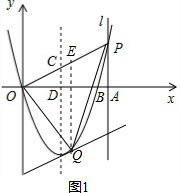
所以当点P与点A重合时,抛物线的解析式为y=x2-4x;
(2)证明:如图1,由已知得P(4,m),则直线OP的解析式为y=$\frac{m}{4}$x,
把P(4,m)代入y=x2+bx得16+4b=m,解得b=$\frac{m-16}{4}$,则抛物线解析式为y=x2+$\frac{m-16}{4}$x,
设直线OP平移后的解析式为y=$\frac{m}{4}$x+n,
∵直线OP平移后的直线与抛物线有且只有一个公共点Q,
∴方程x2+$\frac{m-16}{4}$x=$\frac{m}{4}$x+n有两个相等的实数解,
∴△=42+4n=0,解得n=4,方程的解为x1=x2=2,
∴Q(2,$\frac{1}{2}$m-4),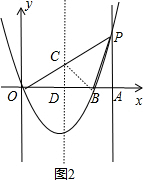
作QE∥y轴交OP于E点,则E(2,$\frac{1}{2}$m),
∴S△OPQ=S△OQE+S△PQE=$\frac{1}{2}$×QE×4=$\frac{1}{2}$×($\frac{1}{2}$m-$\frac{1}{2}$m+4)×4=8,
∴无论m为何值时,△OPQ的面积恒为定值8;
(3)解:存在点P,使得△PBC为直角三角形.
当点P在x轴的上方时,如图1,
若∠PCB=90°,
∵CO=CB,
∴△OCB为等腰直角三角形,
∴∠POB=45°,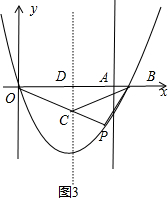
∴PA=OA=4,
∴P(4,4);
若∠PBC=90°,则有∠APB=∠CBD=∠COD,
又∵∠PAB=∠OAP,
∴△PAB∽△OAP,
∴$\frac{AB}{AP}$=$\frac{AP}{OA}$,
∵抛物线的解析式为y=x2+$\frac{m-16}{4}$x,
∴B(4-$\frac{m}{4}$,0),
∴AB=$\frac{m}{4}$,
∴$\frac{\frac{m}{4}}{m}$=$\frac{m}{4}$,
解得:m=1,
∴P(4,1);
当点P在x轴的下方时,如图3,
若∠PCB=90°,
∵CO=CB,
∴∠POB=45°,
∴PA=OA=4,
∴P(4,-4),
若∠CPB=90°,则可证△PAB∽△PAP,
∴$\frac{AB}{AP}$=$\frac{AP}{OA}$,
由上题得B(4-$\frac{m}{4}$,0),
∴AB=-$\frac{m}{4}$
∴$\frac{-\frac{m}{4}}{-m}$=-$\frac{m}{4}$,
解得:m=-1,
综上所述,所求点P的坐标为(4,4)、(4,1)、(4,-4)、(4,-1).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数与一次函数的交点问题和二次函数的性质;理解坐标与图形性质,会利用点的坐标表示相应线段的长;灵活应用相似三角形的判定与性质计算线段的长;会利用分类讨论的思想解决实数问题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | a9 | B. | a6 | C. | a5 | D. | a |
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 80 | 85 | 85 | 80 |
| 方差 | 42 | 42 | 54 | 59 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
| A. | 1 | B. | 4 | C. | 5 | D. | $\sqrt{5}$ |
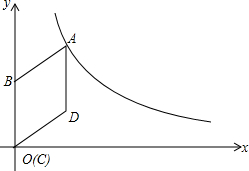 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).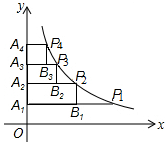 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=a,过点A1,A2,A3,A4分别作y轴的垂线,与反比例函数y=$\frac{2}{x}$(x>0)的图象相交于点P1,P2,P3,P4,过P1,P2,P3,P4分别向A1P1、A2P2、A3P3作垂线,垂足分别为B1、B2、B3,连接P1P2、P2P3、P3P4、将△B1P1P2、△B2P2P3、△B3P3P4面积分别记为S1、S2、S3,则S1+S2+S3=$\frac{3}{4}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=a,过点A1,A2,A3,A4分别作y轴的垂线,与反比例函数y=$\frac{2}{x}$(x>0)的图象相交于点P1,P2,P3,P4,过P1,P2,P3,P4分别向A1P1、A2P2、A3P3作垂线,垂足分别为B1、B2、B3,连接P1P2、P2P3、P3P4、将△B1P1P2、△B2P2P3、△B3P3P4面积分别记为S1、S2、S3,则S1+S2+S3=$\frac{3}{4}$.