题目内容
6. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )| A. | 60° | B. | 65° | C. | 55° | D. | 50° |
分析 根据五边形的内角和等于540°,由∠A+∠B+∠E=300°,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.
解答 解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=540°-300°=240°,
∵∠BCD、∠CDE的平分线在五边形内相交于点P,
∴∠PDC+∠PCD=$\frac{1}{2}$(∠BCD+∠CDE)=120°,
∴∠P=180°-120°=60°.
故选:A.
点评 本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
14.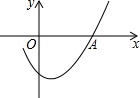 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )| A. | b2<4ac | B. | ac>0 | C. | 2a-b=0 | D. | a-b+c=0 |
15.下列几何体中,主视图、左视图、俯视图完全相同的是( )
| A. | 球 | B. | 圆锥 | C. | 圆柱 | D. | 长方体 |
16.抛物线y=x2-2x+m(m>0)与x轴分别交于点A(x1,0),B(x2,0),点A在点B的左侧,当x=x2-2时,则y的值的取值范围是( )
| A. | y<0 | B. | y≤0 | C. | y>m | D. | y≥m |
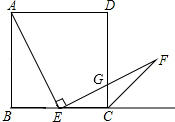 如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.
如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.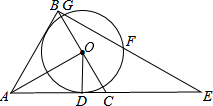 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.