题目内容
16.抛物线y=x2-2x+m(m>0)与x轴分别交于点A(x1,0),B(x2,0),点A在点B的左侧,当x=x2-2时,则y的值的取值范围是( )| A. | y<0 | B. | y≤0 | C. | y>m | D. | y≥m |
分析 由一元二次方程根与系数的关系可求得x1=2-x2>0,可知x=x2-2=-x1<0,结合二次函数的性质可判断出对应y的取值范围.
解答 解:
∵抛物线y=x2-2x+m(m>0)与x轴相交于点A(x1,0),B(x2,0),
∴x1+x2=2,x1x2=m>0,
∴x1=2-x2>0,
∴又抛物线开口向上,与y轴的交点坐标为(0,m),
∴当x=x2-2时,y>m,
故选C.
点评 本题主要考查抛物线与x轴的交点,掌握抛物线与x轴的交点横坐标与对应方程的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )| A. | 60° | B. | 65° | C. | 55° | D. | 50° |
7.必然事件的概率是( )
| A. | -1 | B. | 0 | C. | 0.5 | D. | 1 |
11.计算(m4+n4)(m2+n2)(m+n)(n-m)的结果是( )
| A. | m8-n8 | B. | m16-n16 | C. | n16-m16 | D. | n8-m8 |
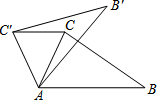 如图,将△ABC绕点A逆时针旋转40°到△AB′C′的位置,则∠ACC′=70°.
如图,将△ABC绕点A逆时针旋转40°到△AB′C′的位置,则∠ACC′=70°.