题目内容
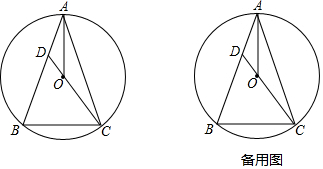
15.已知半径为2的⊙O中,弦AC=2,弦AD=2$\sqrt{2}$,则∠COD的度数为150°或30°.分析 连接OC,过点O作OE⊥AD于点E,由OA=OC=AC可得出∠OAC=60°,再根据垂径定理结合勾股定理可得出AE=OE,即∠OAD=45°,利用角的计算结合圆周角与圆心角间的关系,即可求出∠COD的度数.
解答 解:连接OC,过点O作OE⊥AD于点E,如图所示.
∵OA=OC=AC,
∴∠OAC=60°.
∵AD=2$\sqrt{2}$,OE⊥AD,
∴AE=$\sqrt{2}$,OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{2}$,
∴∠OAD=45°,
∴∠CAD=∠OAC+∠OAD=105°或∠CAD=∠OAC-∠OAD=15°,
∴∠COD=360°-2×105°=150°或∠COD=2×15°=30°.
故答案为:150°或30°.
点评 本题考查了垂径定理、解直角三角形、等边三角形的判定与性质以及圆周角定理,依照题意画出图形,利用数形结合解决问题是解题的关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
10. 一个几何体的三视图如图所示,则这个几何体可能是( )
一个几何体的三视图如图所示,则这个几何体可能是( )
 一个几何体的三视图如图所示,则这个几何体可能是( )
一个几何体的三视图如图所示,则这个几何体可能是( )| A. |  | B. |  | C. |  | D. |  |
20. 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )
 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )| A. |  | B. |  | C. |  | D. |  |
18.经市场调查,某种商品在第x天(1≤x≤90)的售价与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(I)分别求出当1≤x<60和60≤x≤90时,该商品每天利润y与x之间的函数表达式.
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少元?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
| 时间x(天) | 1≤x≤60 | 60≤x≤90 |
| 售价(元/件) | x+40 | 100 |
| 每天销量(件) | 200-2x | |
(I)分别求出当1≤x<60和60≤x≤90时,该商品每天利润y与x之间的函数表达式.
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少元?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.


 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )



 如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.