题目内容
16.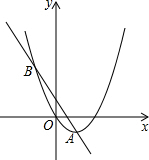 如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )
如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )| A. | 点B的坐标随b的值的变化而变化 | B. | m随x的增大而减小 | ||
| C. | 当m=2时,x=0 | D. | m≥-2 |
分析 将点A的横坐标代入y1=$\frac{1}{2}$x2-2x求得y1=-2,将x=2,y=-2代入y2=-2x+b求得b=2,然后将y1=$\frac{1}{2}$x2-2x与y2=-2x+2联立求得点B的坐标,然后根据函数图形化简绝对值,最后根据函数的性质可求得m的范围.
解答 解:∵将x=2代入y1=$\frac{1}{2}$x2-2x得y1=-2,
∴点A的坐标为(2,-2).
∵将x=2,y=-2代入y2=-2x+b得b=2,
∴y2=-2x+2.
将y1=$\frac{1}{2}$x2-2x与y2=-2x+2联立,解得:x1=2,y1=-2或x2=-2,y2=6.
∴点B的坐标为(-2,6).
故A错误;
∵当x<-2时,y1>y2,
∴m=y1=$\frac{1}{2}$x2-2x.
∴m>6,且m随x的增大而减小.
∵当-2≤x<2时,y1<y2
∴m=y2=-2x+2.
∴-2<m≤6且m随x的增大而减小.
令m=0,求得x=0.
∵当x≥2时,y1>y2,
∴m=y1=$\frac{1}{2}$x2-2x.
∴m≥-2,m随x的增大而增大.
故B错误;
令m=2,求得:x=2+2$\sqrt{2}$.
故C错误.
综上所述,m≥-2.
故选:D.
点评 本题主要考查的是二次函数的性质,根据函数图象比较出y1与y2的大小关系从而得到m的函数关系式是解题的关键.

练习册系列答案
相关题目
8.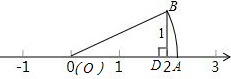 如图,OA=OB,BD=1,则数轴上点A所表示的数为( )
如图,OA=OB,BD=1,则数轴上点A所表示的数为( )
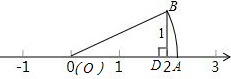 如图,OA=OB,BD=1,则数轴上点A所表示的数为( )
如图,OA=OB,BD=1,则数轴上点A所表示的数为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
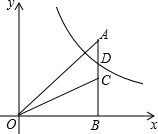 如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B,点C是线段AB上一点,函数y=$\frac{k}{x}$(k>0,x>0)的图象与线段AC交于点D(不与点A、C重合).若△AOB和△COB的面积分别为2和1,则k的值可能是( )
如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B,点C是线段AB上一点,函数y=$\frac{k}{x}$(k>0,x>0)的图象与线段AC交于点D(不与点A、C重合).若△AOB和△COB的面积分别为2和1,则k的值可能是( )