题目内容
6.天虹商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m件与每件的销售价x元满足一次函数关系m=kx+b,当销售单价定为35元时,每天可销售57件;当销售单价定为40元时,每天可销售42件.(1)求m与x的函数关系式;
(2)请写出商场卖这种商品每天的销售利润y元与每件的销售价x元之间的函数关系式;
(3)当每件的销售单价定为多少元时,商场每天所获的利润最高?最高利润为多少?
分析 (1)根据待定系数法解出解析式即可;
(2)根据题意列出函数解析式解答即可;
(3)根据题意列出函数解析式,利用函数解析式的最值解答即可.
解答 解:(1)把x=35,m=57;x=40,m=42代入m=kx+b得,$\left\{\begin{array}{l}{57=35k+b}\\{42=40k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=162}\end{array}\right.$.
故m与x的函数关系式为:m=-3x+162;
(2)根据题意得:y=(-3x+162)(x-30),
即:销售利润y元与每件的销售价x元之间的函数关系式:y=-3x2+252x-4860;
(3)∵y=-3x2+252x-4860=-3(x-42)2+432,
∴当x=42时,y最大=432,
∴每件的销售单价定为42元时,商场每天所获的利润最高,最高利润为432元.
点评 此题考查二次函数的应用,关键是根据题意列出方程和函数解析式,利用函数解析式的最值分析.

练习册系列答案
相关题目
16.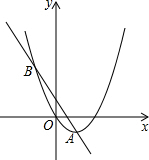 如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )
如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )
 如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )
如图,已知抛物线y1=$\frac{1}{2}$x2-2x,直线y2=-2x+b相交于A、B两点,其中点A的横坐标为2,当x任取一值时,x对应的函数值分别为y1、y2,取m=$\frac{1}{2}$(|y1-y2|+y1+y2)则( )| A. | 点B的坐标随b的值的变化而变化 | B. | m随x的增大而减小 | ||
| C. | 当m=2时,x=0 | D. | m≥-2 |
 如图,在△ABC中,DE∥BC,EF∥AB,若BD:DA=5:3,则CF:CB=5:8.
如图,在△ABC中,DE∥BC,EF∥AB,若BD:DA=5:3,则CF:CB=5:8.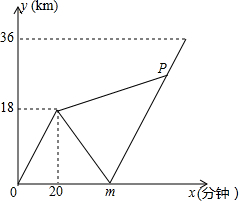 甲、乙两名大学生去距学校36千米的某乡镇进行社会调查,他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回,乙取相机后(在学校取相机所用时间忽略不计)骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两名大学生去距学校36千米的某乡镇进行社会调查,他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回,乙取相机后(在学校取相机所用时间忽略不计)骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为x(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题: