题目内容
4．
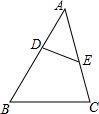如图，在△ABC中，点D，E分别是AB，AC边上的两个点，且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，则S△ADE：S△ABC的值为（ ）| A． | 1：$\sqrt{3}$ | B． | 1：2 | C． | 1：3 | D． | 1：4 |
分析 根据条件$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，和公共角相等可证明△ADE∽△ACB，由相似三角形的性质：对应边的比值相等即可求出DE的长．
解答 解：∵$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，∠A=∠A，
∴△ADE∽△ACB，
∴S△ADE：S△ABC=（$\frac{1}{2}$）2=$\frac{1}{4}$．
故选D．
点评 本题考查了相似三角形的判定和性质，是中考常见题型，比较简单．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图所示，现有一圆心角为90°、半径为80cm的扇形铁片，用它恰好围成一个圆锥形的量筒；如果用其它铁片再做一个圆形盖子把量筒底面密封．（接缝都忽略不计）．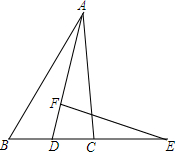
已知：AD是∠BAC的平分线，FE是AD中垂线，求证：ED2=EB•EC．
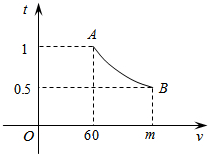一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系：t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A（60，1），和B（m，0.5）
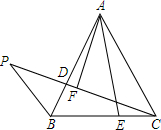已知：等边△ABC，D，E分别是AB，BC上的点，且BD=CE，过点A向CD作垂线，垂足为F，延长CD到点P，连接PB，使∠P=30°，求证：PF=CF．
9．下列说法正确的是（ ）
| A． | 延长射线OP | B． | 延长直线CD | C． | 延长线段CD | D． | 反向延长直线DC |
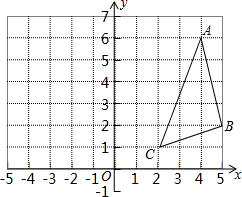如图，△ABC的顶点坐标分别为A（4，6），B（5，2），C（2，1），