题目内容
20. 如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )
如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{17}{8}$ |
分析 作GM⊥BC于M,则GM=AB=1,DG=CM,由矩形的性质得出BC=AD=4,AD∥BC,由平行线的性质得出∠GEF=∠BFE,由折叠的性质得:GF=BF,∠GFE=∠BFE,得出∠GEF=∠GFE,证出EG=FG=BF,设EG=FG=BF=x,求出CM=DG=$\frac{1}{2}$AD=2,得出FM=BC-BF-CM=2-x,在Rt△GFM中,由勾股定理得出方程,解方程即可.
解答 解:作GM⊥BC于M,如图所示: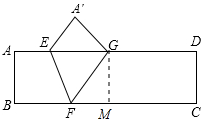
则GM=AB=1,DG=CM,
∵四边形ABCD是矩形,
∴BC=AD=4,AD∥BC,
∴∠GEF=∠BFE,
由折叠的性质得:GF=BF,∠GFE=∠BFE,
∴∠GEF=∠GFE,
∴EG=FG=BF,
设EG=FG=BF=x,
∵G是AD的中点,∴CM=DG=$\frac{1}{2}$AD=2,
∴FM=BC-BF-CM=2-x,
在Rt△GFM中,由勾股定理得:FG2=FM2+GM2,
即x2=(2-x)2+12,
解得:x=$\frac{5}{4}$,即EG=$\frac{5}{4}$;
故选:C.
点评 本题考查了折叠的性质、矩形的性质、平行线的性质、勾股定理、等腰三角形的判定;熟练掌握折叠的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
12.下列方程中,没有实数根的是( )
| A. | x2-6x+9=0 | B. | x2-2x+3=0 | C. | x2-x=0 | D. | (x+2)(x-1)=0 |
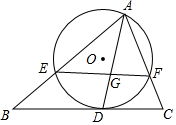 如图,⊙O为△AEF的外接圆,BC与⊙O相切于点D,交AE,AF的延长线于点B,C.AD平分∠BAC,EF交AD于点G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.
如图,⊙O为△AEF的外接圆,BC与⊙O相切于点D,交AE,AF的延长线于点B,C.AD平分∠BAC,EF交AD于点G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.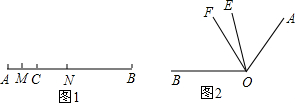
 作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)
作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)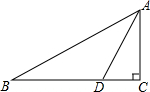 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.