题目内容
17．
如图．点D、E分别是等边△ABC边AB、BC上的点（D、E不与△ABC顶点重合）．且∠DEF=60°，求证：△DBE∽△ECF．
分析 由等边三角形的性质可知∠B=∠C=60°，再由已知条件和三角形内角和定理可证明∠BDE=∠FEC，进而证明△DBE∽△ECF．
解答 证明：∵△ABC是等边三角形，
∴∠B=∠C=60°，
∴∠BDE+∠BED=120°，
∵∠DEF=60°，
∴∠BED+∠FEC=120°，
∴∠BDE=∠FEC，
∴△DBE∽△ECF．
点评 本题考查了相似三角形的判定以及等边三角形的性质，能够结合已知条件和三角形内角和定理证明∠BDE=∠FEC是解题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
已知如图：平面直角坐标系中，A（3，0），B（0，3），AD平分∠BAO．BD⊥AD于D．并连DO，求∠ADO的大小？
如图．已知P为∠ABC平分线上的一点，且PE=PF，结合所学知识，
5．
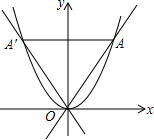如图所示，直线y=2x和y=-2x分别与抛物线y=x2交于点O，A和点0，A′，则下列说法中错误的是（ ）
如图所示，直线y=2x和y=-2x分别与抛物线y=x2交于点O，A和点0，A′，则下列说法中错误的是（ ）| A． | 点A′和点A关于y轴对称 | |
| B． | △AOA′是等腰三角形 | |
| C． | S△AOA′=8 | |
| D． | 线段OA绕点O逆时针旋转60°可与线段OA′重合 |
如图，在锐角△ABC中，已知AB=15，BC=14，AC=13，AD⊥BC于D点，求AD的长．