题目内容
12.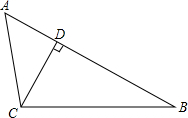 如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证:
如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证:(1)△ACD∽△CDB;
(2)$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$.
分析 (1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD∽△CBD;
(2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°,进一步得出△ADC∽△ACB,△BCD∽△ACB,进一步利用相似的性质得出结论即可.
解答 证明:(1)∵CD是边AB上的高,
∴∠ADC=∠CDB=90°,
∵AC•BD=BC•CD,
∴$\frac{AC}{BC}$=$\frac{CD}{BD}$,
∴△ACD∽△CBD;
(2)∵△ACD∽△CBD,
∴∠A=∠BCD,
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°,
∴△ADC∽△ACB,△BCD∽△ACB,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,$\frac{BC}{AB}$=$\frac{BD}{BC}$,
∴AC2=AB•AD,BC2=AB•BD,
∴$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$.
点评 此题考查了相似三角形的判定与性质,解题的关键是熟记相似三角形的判定定理与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知正比例函数y=kx的图象经过(1,-2)点,则k=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
1.下面是某商场电脑产品的进货单,其中标价一栏被烧掉,请根据其他栏内的信息求出标价.
| 进价 | 标价 | 折扣 | 利润 |
| 3000 | 八折 | 200 |
 已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?
已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小? 如图,AB∥CD,EF⊥DF,∠D:∠E:∠B=4:2:1,求∠E的度数.
如图,AB∥CD,EF⊥DF,∠D:∠E:∠B=4:2:1,求∠E的度数.