题目内容
19．在△ABC中，∠ACB=90°，AB=8，CD为AB边上的中线，则CD的长等于4．分析 根据直角三角形斜边上的中线等于斜边的一半求解即可．
解答 解：∵∠ACB=90°，AB=8，CD为AB边上的中线，
∴CD=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4．
故答案为：4．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在方格纸中．选择一个空白的小正方形涂黑．使其与图中阴影部分构成轴对称图形，则符合要求的小正方形有3个．
如图是由相同大小的小正方体搭成的几何体从不同方向看到的形状图，搭这个几何体共用了4个小正方体．
14．
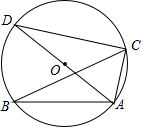如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=25°，则∠CAD的度数是（ ）
如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=25°，则∠CAD的度数是（ ）| A． | 25° | B． | 60° | C． | 65° | D． | 75° |
11．下列数中是无理数的是（ ）
| A． | $-\frac{11}{9}$ | B． | $\sqrt{\frac{1}{4}}$ | C． | $\sqrt{16}$ | D． | $\frac{π}{2}$ |
9．下列语句是命题的是（ ）
（1）两点之间，线段最短；（2）请画出两条互相平行的直线；
（3）过直线外一点作已知直线的垂线；（4）如果两个角的和是90度，那么这两个角互余．
（1）两点之间，线段最短；（2）请画出两条互相平行的直线；
（3）过直线外一点作已知直线的垂线；（4）如果两个角的和是90度，那么这两个角互余．
| A． | （2）（3） | B． | （3）（4） | C． | （1）（2） | D． | （1）（4） |