题目内容
15.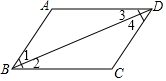 提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.小明提供了如下解答过程:
证明:连结BD.
∵∠1+∠3=180°-∠A,∠2+∠4=180°-∠C,∠A=∠C,
∴∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,请写出正确的证明过程.
(2)用语言叙述上述命题:B.
运用探究:下列条件中,能确定四边形ABCD是平行四边形的是( )
(A)∠A:∠B:∠C:∠D=1:2:3:4 (B)∠A:∠B:∠C:∠D=1:3:1:3
(C)∠A:∠B:∠C:∠D=2:3:3:2 (D)∠A:∠B:∠C:∠D=1:1:3:3.
分析 (1)利用四边形的内角和和已知条件中的对角相等得到邻角互补,从而判定两组对边平行,进而证得结论;
(2)由(1)即可得出结论.
解答 解:(1)正确;理由如下:
∵∠1+∠3=180°-∠A,∠2+∠4=180°-∠C,∠A=∠C,
∴∠1+∠3=∠2+∠4.①
∵∠ABC=∠ADC,
即∠1+∠2=∠3+∠4,②
由①②相加、相减得:∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
(2)∵∠A:∠B:∠C:∠D=1:3:1:3,
∴∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形);
故选:B.
点评 本题考查了平行四边形的判定,解题的关键是了解平行四边形的几个判定定理,难度不大.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
5.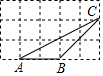 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
20.下列说法正确的是( )
| A. | 五个内角都相等的五边形为正五边形 | |
| B. | 四个内角都是直角的四边形为正四边形 | |
| C. | 六条边都相等的六边形是正六边形 | |
| D. | 每个内角都相等且每条边也相等 |
4. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2∠1+∠2 | C. | 2∠A=∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
5.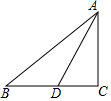 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
 如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )
如图,在Rt△ABC中,∠ACB=90°,AD是BC边上的中线,如果AD=BC,那么tan∠B的值是( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
 甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.
甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是87.5米.