题目内容
1.计算:(1)$\sqrt{{5}^{2}+1{2}^{2}}$
(2)$\sqrt{2{5}^{2}-{7}^{2}}$
(3)$\root{3}{\frac{10}{27}-5}$
(4)$\root{3}{135×25}$.
分析 (1)先算根号里面的平方,再算加法,最后计算算术平方根;
(2)先算平方,再算减法,最后计算算术平方根;
(3)先算根号里面的减法,再计算立方根;
(4)先算根号里面的乘法,再计算立方根.
解答 解:(1)$\sqrt{{5}^{2}+1{2}^{2}}$
=$\sqrt{25+144}$
=$\sqrt{169}$
=13;
(2)$\sqrt{2{5}^{2}-{7}^{2}}$
=$\sqrt{625-49}$
=$\sqrt{576}$
=24;
(3)$\root{3}{\frac{10}{27}-5}$
=$\root{3}{-\frac{125}{27}}$
=-$\frac{5}{3}$;
(4)$\root{3}{135×25}$
=$\root{3}{{3}^{3}×{5}^{3}}$
=3×5
=15.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握平方、算术平方根、立方根等考点的运算.

练习册系列答案
相关题目
12.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1、2、3、4、5,从中随机摸出一个小球,其标号小于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
9.下列计算结果正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D. | $\frac{\sqrt{18}-\sqrt{8}}{2}$=1 |
10.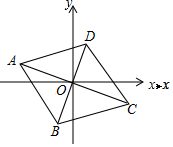 如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
 如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )
如图,平行四边形ABCD的对角线交于坐标原点O.若点A的坐标为(-4,2),则点C坐标为( )| A. | (4,-2) | B. | (4,2) | C. | (2,-4) | D. | (-2,-4) |
 如图,在宽为20m,长30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为504m2,则路宽为多少m?
如图,在宽为20m,长30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为504m2,则路宽为多少m?