题目内容
11.王店某家店公司研制出一种新颖的家用小电器,每件的生产成本为18元,经市场调研表明,按定价40元出售,每日可销售20件.为了增加销量,每降价1元,日销售量可增加2件.若将售价定为x元,日均利润为y元.解答下列问题:(1)求y与x的函数表达式;
(2)当售价定为多少时,日均利润最大,最大利润是多少?
分析 (1)根据日销售利润=每件利润×日销售量得到:y=(x-18)[20+2(40-x)],整理即可;
(2)把W=-2x2+136x-1800配成二次函数的顶点式得到W=-2(x-34)2+512,然后根据二次函数的性质回答即可.
解答 解:(1)y=(x-18)[20+2(40-x)]=-2x2+136x-1800;
(2)y=-2x2+136x-1800
=-2(x-34)2+512,
∵a=-2<0,y有最大值512,
∴当x=34时,y有最大值512元,
所以当每件产品的售价定为34元时,最大月销售利润是512元.
点评 本题主要考查了二次函数的实际应用,审清题意列出函数表达式,熟悉二次函数的性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
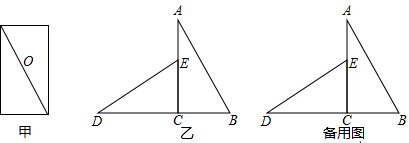
 如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为8cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F在AD上,若△ABC的面积为16cm2,则图中阴影部分的面积为8cm2.