题目内容
19.若不等式$\left\{\begin{array}{l}{x-a≥0}\\{2x-3<1}\end{array}\right.$有两个整数解,则a的取值范围是-1<a≤0.分析 先求出每个不等式的解集,再求出不等式组的解集,即可得出关于a的不等式组即可.
解答 解:$\left\{\begin{array}{l}{x-a≥0①}\\{2x-3<1②}\end{array}\right.$
∵解不等式①得:x≥a,
解不等式②得:x<2,
∴不等式组的解集为a≤x<2,
∵不等式$\left\{\begin{array}{l}{x-a≥0}\\{2x-3<1}\end{array}\right.$有两个整数解,
∴-1<a≤0,
故答案为:-1<a≤0.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,解此题的关键是能根据不等式组的整数解和已知得出关于a的不等式组.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
9.若mx<m,得x>1,则应为( )
| A. | m<0 | B. | m>0 | C. | m≤0 | D. | m≥0 |
10.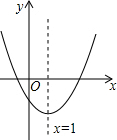 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
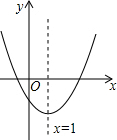 已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )
已知y=ax2+bx+c(a≠0)在平面直角坐标系中的图象如图所示,则下列结论正确的是( )| A. | a<0 | B. | c>0 | C. | 2a+b=0 | D. | 4a+2b+c>0 |
14.下列各图是电视台的台徽,其中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8. 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )
 如图,a∥b,∠1=120°,则∠2等于( )
如图,a∥b,∠1=120°,则∠2等于( )| A. | 30° | B. | 90° | C. | 60° | D. | 50° |
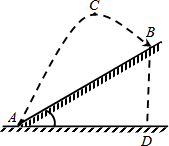 如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞?
如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞? 如图,在等腰Rt△ABC中,∠ACB=90°,以斜边AB为x轴建立直角坐标系上,点C(1,4)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在等腰Rt△ABC中,∠ACB=90°,以斜边AB为x轴建立直角坐标系上,点C(1,4)在反比例函数y=$\frac{k}{x}$的图象上. 如图,△ABC≌△ADE,∠E=∠DAB,找出图中平行的两条线段,并说明理由.
如图,△ABC≌△ADE,∠E=∠DAB,找出图中平行的两条线段,并说明理由.